Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 172

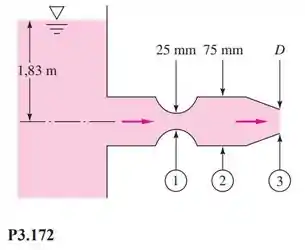
O escoamento de água a 35°C da Figura P3.172 descarrega para a atmosfera padrão ao nível do mar. Desprezando as perdas, para qual diâmetro D do bocal começa a ocorrer cavitação? Para evitar a cavitação, você deve aumentar ou diminuir D com relação a esse valor crítico?

Passo 1

Para resolver está questão vamos começar encontrando a velocidade em 3. Para isto basta aplicar Bernoulli entre um ponto na superfície da água no reservatório (ponto 4). Só temos que lembrar que o reservatório está aberto e que o escoamento descarrega para a atmosfera, logo, p 4 = p 3 = p a t m , e, devido ao diâmetro do reservatório V 4 = 0 .

Aplicando na equação de Bernoulli (vamos adotar o referencial de altura em 3 como zero):

p 3 + ρ 2 V 3 2 + ρ g z 3 = p 4 + ρ 2 V 4 2 + ρ g z 4

p a t m + ρ 2 V 3 2 + = p a t m + ρ g z 4

V 3 2 2 = 1,82 * 9,81

V 3 = 5,98 m s

Passo 2

Agora vamos aplicar Bernoulli entre 1 e 3 para podermos encontrar V 1 . Como em 1 ocorre cavitação a pressão será igual a pressão de vapor da água a 35°C, ou seja, p 1 = 5600   P a . A diferença de altura entre 1 e 3 é zero.

Aplicando a equação de Bernoulli:

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 3 + ρ 2 V 3 2 + ρ g z 3

p 1 + ρ 2 V 1 2 = p a t m + ρ 2 V 3 2

5600 + 1000 2 V 1 2 = 101325 + 1000 2 * 5,98 2

V 1 = 15,07 m s

Passo 3

Agora só precisamos de alguma expressão que utilize os dados que temos e o diâmetro em 1. A equação que podemos utilizar para isto é a da continuidade entre 1 e 3:

Q 1 = Q 3

V 1 * A 1 = V 3 * A 3

V 1 π 4 D 1 2 = V 3 π 4 D 3 2

D 3 = V 1 D 1 2 V 3 = 15,07 * 25 1000 2 5,98 = 0,040   m

Ou seja, este é o valor em que começa ocorrer cavitação. Para evitar a cavitação o diâmetro deve ser inferior, ou seja, D 3 < 0,040   m , pois assim o sistema mantém a pressão em 1 maior que a pressão de vapor da água.

Resposta

A cavitação começa quando D 3 = 0,040   m . Para evitar a cavitação o diâmetro deve ser menor que 0,040 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando uma bomba manual de bicicleta para gerar jato de ar, uma lata de refrigerante como reservatório de água e um canudinho como tubo, projete e construa um atomizador. Estude os efeitos dos diverso
Usando um balde grande cujo volume é conhecido e medindo o tempo necessário para preencher o balde com água por meio de uma mangueira de jardim, determine a vazão em massa e a velocidade média da água
Reconsidere o Problema 5-89. Para drenar o tanque mais rapidamente, uma bomba é instalada próximo à saída do tanque. Determine a entrada de carga necessária na bomba para estabelecer uma velocidade mé
Ar a 110k P a e 50 ° C escoa para data através de um tubo inclinado com 6c m de diâmetro a uma vazão de 45L / s . O diâmetro do duto é reduzido para 4c m por meio de um redutor. A variação de pressão
Para as condições do Problema 3.127, se a central não puder aquecer a água do rio vizinho além de 12 ° C, qual deverá ser a vazão mínima Q, em m³/s, através do trocador de calor da central? Como o val