Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 49

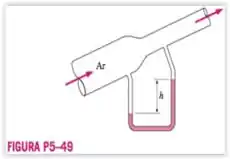
Ar a 110   k P a e 50 ° C escoa para data através de um tubo inclinado com 6   c m de diâmetro a uma vazão de 45   L / s . O diâmetro do duto é reduzido para 4   c m por meio de um redutor. A variação de pressão através do redutor é medida por um manômetro de água. A diferença de elevação entre os dois pontos do tubo onde os dois braços do manômetro estão ligados é de 0,20   m . Determine a altura diferencial entre os níveis de fluido dos dois braços do manômetro.

Passo 1

Temos um tubo inclinado com suas determinadas particularidades e a ele está conectado um manômetro, os pontos que iremos avaliar são:

Podemos dizer que os pontos 1 e 2 estão em contato com a pressão que é do ar, mas assim como a velocidade, serão diferentes uma vez que no ponto 1 as linhas de corrente são mais afastadas (velocidade e pressão menor), já no ponto 2 temos linhas de corrente mais próximas (velocidade e pressão maior). Por fim, não temos um ponto de referência a ser considerado.

Vamos utilizar a equação de Bernoulli, pois não temos componentes complexos:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

P 1 ρ g - P 2 ρ g = V 2 2 2 g - V 1 2 2 g

P 1 - P 2 = ρ V 2 2 - V 1 2 2

Passo 2

Temos as referências para calcular a densidade do ar, para essa pressão e temperatura a constante do ar é R = 0,287   k P a   m 3 k g K :

ρ = P R T

ρ = 110   k P a 0,287   k P a   m 3 k g K × 50 + 273 K = 1,187 k g m 3

Pela formula da vazão ( v ˙ = π D 2 4 × V ) podemos encontrar cada velocidade:

V 1 = 4 v ˙ π D 2 = 4 × 0,045 m 3 s π ( 0,06 ) 2 = 15,92 m s

V 2 = 4 v ˙ π D 2 = 4 × 0,045 m 3 s π ( 0,04 ) 2 = 35,81 m s

Passo 3

Já temos a velocidade agora só falta a diferença de pressão:

P 1 - P 2 = 1,187 k g m 3   × 35,81 2 - 15,92 2 m s   2

P 1 - P 2 = 1,187 k g m 3   × 1028,9097   2 = 610,7   P a

Como estamos tratanto de um manômetro, podemos utilizar a seguinte formula para encontrarmos a altura:

∆ P = ρ g h

610,7   P a = 1,187 k g m 3   × 9,8 m s 2 × h

h = 52,5   m

Prontinho!!

Resposta

h = 52,5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o coeficiente α da energia cinética para o escoamento de um líquido num tubo de seção circular. O escoamento é laminar e o diagrama de velocidades é v = v m a x 1 - r R 2 .
No circuito da figura, a bomba B 1 é acionada pela turbina. A vazão é 30 L/s e os rendimentos da turbina e da bomba B 1 são, respectivamente, 0,7 e 0,8. A perda de carga na tubulação é 15 m. Sabendo q
Sabendo que a vazão proporcionada pelo tanque inferior da instalação é igual a 15 L/s e que a potência dissipada por atritos em toda a instalação é 1 kW, determinar o tipo da máquina e sua potência. D
É dado um diagrama bidimensional de velocidades de um fluido ideal, num canal de largura de 2 m:a) Qual a velocidade média na seção?b) Qual é a vazão em volume?c) Qual é o coeficiente α da energia cin
Airflow at Ma 5 2.8, p 5 80 kPa, and T 5 280 K undergoes a 158 compression turn. Find the downstream valuesof (a) Mach number, (b) pressure, and (c) temperature.