Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 173

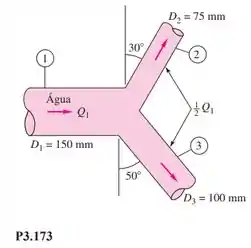
O acessório horizontal em Y da Figura P3.173 divide em partes iguais a vazão de água a 20°C. Se Q 1 = 142   L / s , p 1 = 172,4   k P a (manométrica) e as perdas são desprezadas, calcule (a) p 2 , (b) p 3 e (c) o vetor da força necessária para manter o Y no lugar.

Passo 1

Para revolver essa questão vamos começar encontrando as velocidades em 1, 2 e 3, lembrando que em 2 e 3 a vazão é Q 2 = Q 3 = Q 1 2 , sendo que Q 1 = 142 L s = 0,142 m 3 s .

A velocidade pode ser escrita como:

V = Q A

Em 1:

V 1 = Q 1 A 1 = Q 1 π 4 D 1 2 = 0,142 3,14 4 * 150 1000 2 = 8,04 m s

Em 2:

V 2 = Q 2 A 2 = Q 2 π 4 D 2 2 = 0,142 2 3,14 4 * 75 1000 2 = 16,07 m s

E em 3:

V 3 = Q 3 A 3 = Q 3 π 4 D 3 2 = 0,142 2 3,14 4 * 100 1000 2 = 9,04 m s

Passo 2

Agora vamos aplicar Bernoulli entre 1 e 2 e entre 1 e 3 para encontramos p 2 e p 3 , respectivamente. Vamos considerar que as diferenças de altura entre 1 e 2 e entre 1 e 3 são nulas.

Para os pontos 1 e 2:

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 2 + ρ 2 V 2 2 + ρ g z 2

p 1 + ρ 2 V 1 2 = p 2 + ρ 2 V 2 2

  172400 + 1000 2 8,04 2 = p 2 + 1000 2 16,07 2

p 2 = 75598,35   P a

Para os pontos 1 e 3:

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 3 + ρ 2 V 3 2 + ρ g z 3

p 1 + ρ 2 V 1 2 = p 3 + ρ 2 V 3 2

  172400 + 1000 2 8,04 2 = p 3 + 1000 2 9,04 2

p 3 = 163860   P a

Passo 3

Para calcular o vetor da força necessária para manter o Y no lugar, vamos precisar analisar as forças em x e y.

O somatório de forças em x é:

∑ F x = R x + p 1 A 1 - p 2 s e n ( θ ) A 2 - p 3 s e n ( θ ) A 3

Onde R x representa a força que mantém o Y no lugar na direção x.

Agora é só lembrar que ∑ F x = - m ˙ V 1 + m ˙ V 2 s e n ( θ ) + m ˙ 3 V 3 s e n ( θ ) e substituir:

- m ˙ 1 V 1 + m 2 ˙ V 2 s e n ( θ ) + m ˙ 3 V 3 s e n ( θ ) = R x + p 1 A 1 - p 2 s e n θ A 2 - p 3 s e n θ A 3

Como m ˙ = ρ Q = 1000 * 0,142 = 142 k g s :

- 8,04 * 142 + 16,07 * s e n 30 ° * 142 2 + 9,04 * s e n 50 ° * 142 2 = R x + 3,14 4 * 1000 2 172400 * 150 2 - 75598,35 * s e n 30 ° * 75 2 - 163860 * s e n 50 ° * 100 2

- 76,9782 = R x + 1888,61

R x = - 1965,58   N

Agora, fazendo para y, teremos:

m 2 ˙ V 2 c o s θ - m ˙ 3 V 3 c o s θ = R y - p 2 c o s θ A 2 + p 3 c o s θ A 3

16,07 * c o s 30 ° * 142 2 - 9,04 * c o s 50 ° * 142 2 = R y + 3,14 4 * 1000 2 - 75598,35 * c o s 30 ° * 75 2 + 163860 * c o s 50 ° * 100 2

577,33 = R y + 534,41

R y = 42,92   N

Resposta

Letra a) p 2 = 75598,35   P a ;

Letra b) p 3 = 163860   P a ;

Letra c) R = - 1965,58   ,   42,92   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O veículo com sustentação pneumática da Figura P3.160 admite ar padrão ao nível do mar através de um ventilador e o descarrega em alta velocidade através de uma borda anular de 3 cm de folga. Se o veí
Um tubo convergente-divergente, chamado Venturi, desenvolve um escoamento de baixa pressão na garganta capaz de aspirar fluido para cima de um reservatório, como na Figura P3.161. Aplicando a equação
Um medidor Venturi, mostrado na Figura P3.165, tem uma redução de seção cuidadosamente projetada cuja diferença de pressão é uma medida da vazão no tubo. Aplicando a equação de Bernoulli para escoamen
Na Figura P3.164, o jato aberto de água a 20°C sai de um bocal para o ar ao nível do mar e atinge um tubo de estagnação, como mostra a figura. Se a pressão na linha de centro na seção 1 é 110 kPa e as
O tanque de água cilíndrico na Figura P3.159 está sendo abastecido com uma vazão volumétrica Q 1 = 3,79 L m i n , enquanto a água é também drenada por um furo na parte inferior de diâmetro d = 6m m .