Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 16

Dados: H p 2,3 = 2   m ; A 3 = 20   c m 2 ; A 2 = 1   c m 2 ; H p 0,1 = 0,8   m ; η B = 70 % . Determinar:

  1. a vazão ( L / s ) ;
  2. a área da seção 1 c m 2 ;
  3. a potência fornecida pela bomba ao fluido.

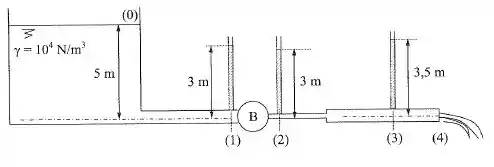
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Aplicando Bernoulli entre os pontos 2 e 3 , temos que:

z 2 + v 2 2 2 g + P 2 γ = z 3 + v 3 2 2 g + P 3 γ + H p 2,3

Rearranjando, temos que:

v 2 2 - v 3 2 = 2 g P 3 γ - P 2 γ + H p 2,3

Substituindo os valores e resolvendo, temos que:

v 2 2 - v 3 2 = 20 3,5 - 3 + 2

v 2 2 - v 3 2 = 50

Passo 2

Pela equação da continuidade sabemos que:

v 2 A 2 = v 3 A 3

Logo:

v 2 = v 3 A 3 A 2

v 2 = 20 v 3

Portanto:

20 v 3 2 - v 3 2 = 50

v 3 = 0,354   m / s

E:

v 2 = 7,1   m / s

A vazão será então:

Q = 7,1 ⋅ 10 - 4

Q = 0,71   L / s

Passo 3

Aplicando Bernoulli entre os pontos 0 e 1 , temos que:

z 0 = v 1 2 2 g + P 1 γ + z 1 + H p 0,1

Isolando a velocidade, teremos:

v 1 = 2 g z 0 - P 1 γ - H p 0,1

Substituindo os valores, temos que:

v 1 = 20 5 - 3 - 0,8

v 1 = 4,9   m / s

Podemos então encontrar a área da seção 1 :

A 1 = Q v 1

A 1 = 0,71 ⋅ 10 - 3 4,9

A 1 = 1,45   c m 2

Passo 4

A perda de carga da bomba é calculada por:

H B = v 2 2 - v 1 2 2 g

H B = 7,1 2 - 4,9 2 20

H B = 1,32   m

Com a perda de carga definida, é possível obter a potência necessária:

N = γ Q H B

Substituindo os valores, temos que:

N = 10 4 ⋅ 0,71 ⋅ 10 - 3 ⋅ 1,32

N = 9,4   W

Resposta

a )   Q = 0,71   L / s

b ) A 1 = 1,45   c m 2

c )   N = 9,4   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a potência da bomba é 3k W , seu rendimento 75 % e que o escoamento é de 1 para 2 , determinar:A vazão;A carga manométrica da bomba;A pressão do gás.Dados: H p 1,2 = H 5,6 = 1,5m ; H p 3,4
Quais são as vazões de óleo em massa e em peso no tubo convergente da figura, para elevar uma coluna de 20c m de óleo no ponto ( 0 ) ?Dados: desprezar as perdas; γ ó l e o = 8000N / m 3 ó ; g = 10m /
Na instalação da figura, a carga total na seção 2 é 12m . Nessa seção, existe um piezômetro que indica 5m . Dados: γ H 2 O = 10 4N / m 3 ; γ H g = 1,36 × 10 5N / m 3 ; h = 1m ; D 1 = 6c m ; D 2 = 5c m
Um dos métodos para se produzir vácuo numa câmara é descarregar água por um tubo convergente-divergente, como é mostrado na figura. Qual deve ser a vazão em massa de água pelo convergente-divergente,
No conduto da figura, o fluido é considerado ideal. Dados: H 1 = 16m ; P 1 = 52k P a ; γ = 10 4N / m 3 ; D 1 = 10c m .Determinar:A vazão em peso;A altura h 1 no manômetro;O diâmetro da seção ( 2 ) .