Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 33

Um escoamento é descrito pelo campo de velocidade V =   a x i   +   b j , em que a   =   1 / 5   s   - 1 b   =   1   m / s . As coordenadas são medidas em metros. Obtenha uma equação para a linha de corrente que passa através do ponto ( 1 ,   1 ) . Em t   =   5   s , quais são as coordenadas da partícula que passou pelo ponto ( 1 ,   1 ) em t   =   0 ? Quais são suas coordenadas em t   =   10   s ? Trace a linha de corrente e as posições da partícula no início, em 5   s e 10   s . Que conclusões você pode tirar sobre trajetória, linha de corrente e linha de emissão para este escoamento?

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, temos que encontrar a equação para as linhas de corrente, para isso, temos:

v u = d y d x = b a x

Separando as variáveis e integrando:

d x x = a b d y a b y - y 0 = ln ⁡ x x 0

A solução é dada por:

y = y 0 + b a ln ⁡ x x 0 y = 5 ln ⁡ x + 1

Passo 2

Agora, para determinarmos a trajetória, vamos encontrar x ( t ) :

d x d t = u = a x v = d y d t = b

Separando as variáveis e integrando:

d x x = a   d t ln ⁡   x x 0 = a t - t 0  

d y = b   d t

y = y 0 + b ( t - t 0 )

Logo, as trajetórias são dadas por:

x t t = x 0 e a t - t 0 y t ( t ) = y 0 + b ( t - t 0 )

Com isso, precisamos encontrar a posição da partícula nos instantes pedidos. Para x 0 , y 0 = ( 1,1 ) , t 0 = 0 e t = 1   s , temos:

x t t = x 0 e a t - t 0 = e 1 / 5   m y t t = y 0 + b t - t 0 = 2   m

Para x 0 , y 0 = ( 1,1 ) , t 0 = 0 e t = 5   s :

x t t = x 0 e a t - t 0 = e y t t = y 0 + b t - t 0 = 6   m

E para x 0 , y 0 = ( 1,1 ) , t 0 = 0 e t = 10   s   :

x t t = x 0 e a t - t 0 = e 2   m y t t = y 0 + b t - t 0 = 11   m

Passo 3

Por fim, nosso gráfico fica assim:

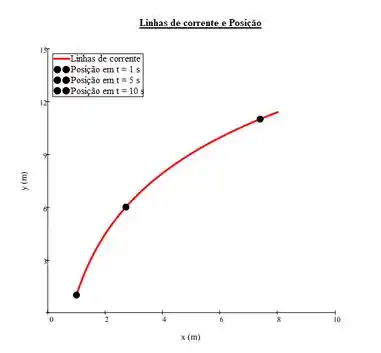
Resposta

x t 1 = e 1 / 5   m y t 1 = 2   m

x t 5 = e y t 5 = 6   m

x t 10 = e 2   m y t 10 = 11   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa quadrada de 1,0m de lado e 20N de peso desliza sobre um plano inclinado de 30 ° , sobre uma película de óleo. A velocidade da placa é 2m / s constante. Qual é a viscosidade dinâmica do óleo,
São dadas duas placas planas paralelas à distância de 2m m . A placa superior move-se com velocidade de 4m / s , enquanto a inferior é fixa. Se o espaço entre as duas placas for preenchido com óleo (
O pistão da figura tem uma massa de 0,5k g . O cilindro de comprimento ilimitado é puxado para cima com velocidade constante. O diâmetro do cilindro é 10c m e do pistão é 9c m e entre os dois existe u
O dispositivo da figura é constituído de dois pistões de mesmas dimensões geométricas que se deslocam em dois cilindros de mesmas dimensões. Entre os pistões e os cilindros existe um lubrificante de v