Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 6
O pistão da figura tem uma massa de . O cilindro de comprimento ilimitado é puxado para cima com velocidade constante. O diâmetro do cilindro é e do pistão é e entre os dois existe um óleo de e . Com que velocidade deve subir o cilindro para que o pistão permaneça em repouso? (Supor diagrama linear e .)
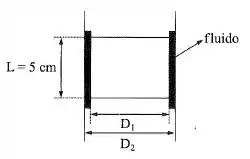
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Antes de calcularmos a velocidade do cilindro, deveremos fazer as seguintes manipulações:
Logo:
Isolando para a velocidade, temos que:
Passo 2
Agora que encontramos uma equação para resolver nosso problema, temos que encontrar as variáveis dessa equação. Temos que:
Temos também que:
Passo 3
Agora é só substituir na equação do . Temos que:
Resolvendo, temos que a velocidade do cilindro é dada por:
Resposta
Exercícios de Livros Relacionados
O turbocompressor de um motor de combustão interna tem uma rotação de 120.000r p m ω = 2 π n . Os mancais do eixo são flutuantes e giram com uma certa rotação. São dados: μ = 8 × 10 - 3N ⋅ s / m 2 ; D
Assumindo o diagrama de velocidades indicado na figura, em que a parábola tem seu vértice a 10c m do fundo, calcular o gradiente de velocidade e a tensão de cisalhamento para y = 0 ; 5 ; 10c m . Adota
Na figura, uma placa de espessura desprezível e área A 1 = 2m 2 desloca-se com v = 5m / s constante, na interface de dois fluidos, tracionada por uma força F = 400N . Na parte superior, ε = 1m m e o d
UmcampodevelocidadeéespecificadocomoemqueV → = a x y i ^+ b y 2 j ^ emquea=2m−1s−1,b=−6m−1s−1eascoordenadassão medidasemmetros.Ocampodeescoamentoéuni,bioutridimensional?Porquê?Calculeascomponentesdave
Para o campo de velocidade em que V → = A x 2 y i ^ + B x y 2 j ^ , em que A = 2m - 2 s - 1 e B = 1m - 2 s - 1 , e as coordenadas são medidas em metros, obtenha uma equação para as linhas de corrente