Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 4
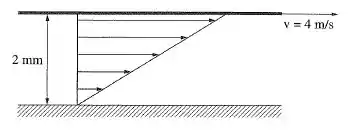
São dadas duas placas planas paralelas à distância de . A placa superior move-se com velocidade de , enquanto a inferior é fixa. Se o espaço entre as duas placas for preenchido com óleo , qual será a tensão de cisalhamento que agirá no óleo?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para descobrir a viscosidade dinâmica temos a seguinte equação:
Onde:
: Viscosidade Dinâmica
: Viscosidade Cinemática
: Massa Específica
Portanto:
Passo 2
Sabendo que a lei de Newton da viscosidade é dada por uma proporcionalidade entre a tensão de cisalhamento e do gradiente de velocidade, temos a seguinte equação:
Substituindo os valores, temos que:
A tensão de cisalhamento será:
Resposta
Exercícios de Livros Relacionados
O eixo da figura, ao girar, provoca a rotação do tambor. Este enrola a corda, que levanta um peso de 10N com uma velocidade constante de 0,5m / s . O fluido existente entre o eixo e o tambor tem μ = 0
Dois discos são dispostos coaxialmente face a face, separados por um filme de óleo lubrificante de espessura ε pequena. Aplicando-se um momento no disco 1 , ele inicia um movimento em torno de seu eix
No sistema da figura, o corpo cilíndrico de peso G desce com velocidade constante v = 2m / s , fazendo o eixo girar. Dados μ = 10 - 3N ⋅ s / m 2 ; L = 2 / πm ; D e = 50,2c m ; D i = 50c m ; d = 10c m
A placa da figura tem uma área de 4m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa, formando um diagrama de velocidades dado por v = 20 y v m á x 1 - 5 y á . A viscosida
Um fluido escoa sobre uma placa com o diagrama dado. Pede-se v = f y ;A tensão de cisalhamento junto à placa.