Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 23

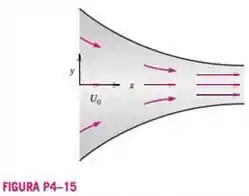
O escoamento de duto convergente (Figura P4-15) é modelado pelo campo de velocidade estacionário e bidimensional do Problema 4-15. Gere uma expressão analítica para as linhas de corrente do escoamento.

Passo 1

A questão pede que a gente ache uma equação que represente as curvas, conhecidas como linhas de corrente, de um escoamento. Esse escoamento já foi estudado no problema 4-15. A velocidade de cada partícula de fluido desse escoamento pode ser calculada pela equação abaixo.

V → = U 0 + b ⋅ x ⏟ u ⋅ i → - b ⋅ y ⏟ v ⋅ j →

onde u é a componente do eixo x da velocidade V → , v é a componente do eixo y da velocidade V → . Isso quer dizer que para esse escoamento bidimensional no plano x y :

u = U 0 + b ⋅ x

v = - b ⋅ y

No próximo passo, vamos entender como usar essa informação para determinar a equação das linhas de corrente.

Passo 2

O primeiro passo para transformar as equações de u e v na equação das linhas de corrente é usar a equação 4 - 16 do livro que está abaixo. Ela mostra a relação entre a inclinação das linhas de corrente d y d x , u e v .

d y d x = v u       ⟹       d y d x = - b ⋅ y U 0 + b ⋅ x

Reorgazinando a equação acima, encontramos:

d y d x = - b ⋅ y U 0 + b ⋅ x       ⟹       d y - b ⋅ y = d x U 0 + b ⋅ x

Passo 3

Integrando os dois lados da equação, achamos:

∫ - d y b ⋅ y = ∫ d x U 0 + b ⋅ x       ⟹     - 1 b ⋅ ln ⁡ y = 1 b ⋅ ln ⁡ U 0 + b ⋅ x + K

onde K é uma constante de integração.

Continuando o desenvolvimento dessa equação:

ln ⁡ y = - ln ⁡ U 0 + b ⋅ x - b ⋅ K       ⟹       y = e - ln ⁡ U 0 + b ⋅ x - b ⋅ K       ⟹       y = e ln ⁡ U 0 + b ⋅ x - 1 ⋅ e - b ⋅ K

y = e - b ⋅ K ⏞ C U 0 + b ⋅ x       ⟹       y = C U 0 + b ⋅ x

onde C é outra constante criada a partir de K .

Resposta

y = C U 0 + b ⋅ x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cite pelo menos três outros nomes para a derivada material e escreva uma breve explicação sobre o motivo pelo qual cada nome é apropriado.
Considere a visualização do escoamento ao redor da esfera na Figura P4-29C. Estamos vendo linhas de corrente, linhas de emissão, linhas de trajetória ou linhas de tempo? Explique.Visualização do escoa
Considere a visualização do escoamento de um vórtice em efeito solo na Figura P4-29C. Estamos vendo linhas de corrente, linhas de emissão, linhas de trajetória ou linhas de tempo? Explique.Visualizaçã
Qual é a definição de uma linha de trajetória? O que indicam as linhas de trajetória?
Considere a visualização do escoamento em uma asa-delta com abertura de 15° na Figura P4-27C. Estamos vendo linhas de corrente, linhas de emissão, linhas de trajetória ou linhas de tempo? Explique.Vis