Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 25

Qual é a definição de uma linha de trajetória? O que indicam as linhas de trajetória?

Passo 1

Para entender a definição de linhas de trajetória, vamos imaginar uma mangueira injetando partículas coloridas de água misturada com tinta em um escoamento de água através de um canal. A ponta da mangueira fica mudando de direção. Isso significa que a cada momento a mangueira injeta uma partícula colorida com uma velocidade em sentido diferente. A figura abaixo mostra esse exemplo.

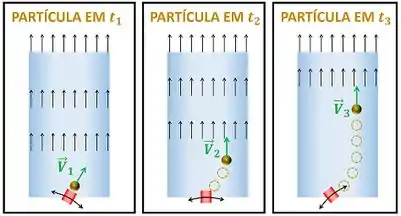
A figura acima mostra a mangueira (ponta vermelha) que joga água com tinta no escoamento. Essa figura também mostra o trajeto que essa única partícula de água com tinta faz ao longo do escoamento.

Passo 2

A soma de todos os pontos do trajeto dessa partícula forma uma linha no escoamento. Essa linha é a linha de trajetória da partícula.

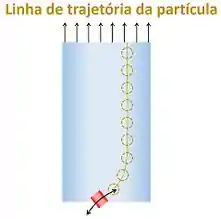
Ou seja, a linha de trajetória indica o trajeto percorrido por uma partícula de fluido no escoamento.

Resposta

Uma linha de trajetória é a trajetória real percorrida por uma partícula de fluido

individual em determinado período de tempo. Elas indicam o trajeto de uma partícula de fluido em um escoamento.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Existem várias ocasiões em que um escoamento de corrente livre razoavelmente uniforme encontra um cilindro longo normal ao escoamento (Figura P4-94). Os exemplos incluem o ar ecoando ao redor de uma a

Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y

Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule ε r θ , a taxa de deformação por cisalhamento no plano r θ . Discuta se as partículas de fluido desse

Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo

Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma