Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 65

Um escoamento incompressível bidimensional é definido por

u = K y x 2 + y 2 ; v = K x x 2 + y 2

em que K = constante. Esse escoamento é irrotacional? Em caso afirmativo, encontre seu potencial de velocidade, faça um esboço de algumas linhas equipotenciais e interprete o padrão de escoamento.

Passo 1

Bora que essa é fácil!

Vamos checar se o escoamento é irrotacional:

ω z = 1 2 ∂ v ∂ x - ∂ u ∂ y

2 ω z = K x 2 + y 2 - 2 K x 2 x 2 + y 2 2 + K x 2 + y 2 - 2 K y 2 x 2 + y 2 2 =

= 2 K x 2 + y 2 - 2 K x 2 + y 2 x 2 + y 2 2 = 0

Portanto o escoamento é irrotacional. Então podemos encontrar seu potencial de velocidade:

u =   ∂ ϕ ∂ x = - K y x 2 + y 2 ; v =   ∂ ϕ ∂ y = K x x 2 + y 2  

Integrando as equações e igualando-as:

ϕ = K t a n - 1 y x + c y = K t a n - 1 y x + c x

Daí:

ϕ = K t a n - 1 y x = k θ

Plotando-a:

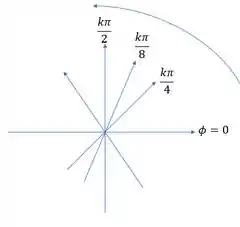
Resposta

O escoamento é irrotacional e seu potencial de velocidade é:

ϕ = k θ

Conforme o gráfico abaixo o escoamento representa um vórtex que tem sentido anti-horário.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The Flettner rotor sailboat in Fig. E8.3 has a water dragcoefficient of 0.006 based on a wetted area of 45 ft2. If therotor spins at 220 r/min, fi nd the maximum boat velocitythat can be achieved in a
Hurricane Sandy, which hit the New Jersey coast on Oct.29, 2012, was extremely broad, with wind velocities of40 mi/h at 400 miles from its center. Its maximum velocitywas 90 mi/h. Using the model of F
Consider potential fl ow of a uniform stream in the x direction plus two equal sources, one at (x, y) 5 (0, 1a) and theother at (x, y) 5 (0, 2a). Sketch your ideas of the bodycontours that would arise
Starting at the stagnation point in Fig. 8.6, the fluid acceleration along the half-body surface rises to a maximumand eventually drops off to zero far downstream. (a) Doesthis maximum occur at the po
A proposed harmonic function F(x, y, z) is given byF 5 2x2 1 y3 2 4xz 1 f(y)(a) If possible, fi nd a function f (y) for which the laplacianof F is zero. If you do indeed solve part (a), can your final