Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 5
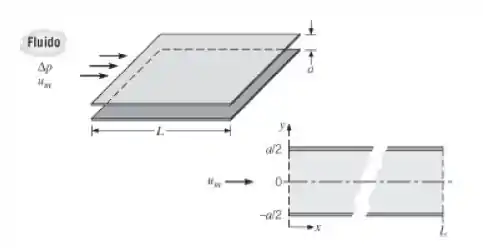
Para o escoamento laminar plenamente desenvolvido através de um canal entre placas paralelas, o componente na direção x da equação do momento tem a forma:
O objetivo deste problema é desenvolver expressões para a distribuição de velocidades e o gradiente de pressão análogas àquelas para o tubo circular na Seção 8.1.
- Mostre que o perfil de velocidades, , é parabólico e tem a forma:
- Escreva uma expressão definindo o fator de atrito, f, usando como comprimento característico o diâmetro hidráulico . Qual é o diâmetro hidráulico para o canal de placas paralelas?
- O fator de atrito é estimado com a expressão , com C sendo uma função da seção transversal do escoamento, como mostrado na Tabela 8.1. Qual é o coeficiente C para o escoamento entre placas?
- Ar escoa em um canal entre placas paralelas com uma separação entre placas de 5 mm e um comprimento de 200 mm, apresentando uma queda de pressão de . Calcule a velocidade média e o número de Reynolds para o ar na pressão atmosférica e a 300 K. A hipótese de escoamento plenamente desenvolvido é razoável nessa aplicação? Se não, qual é o efeito na estimativa de ?
na qual é a velocidade média:
E , com Δp sendo a queda de pressão ao longo do canal com comprimento L.
Passo 1
Vaaaamo que vaaaamoo, galerinhaa ?!
Estamos aqui a todo vapor!!
Para a letra (a) nós vamos precisar da equação dada:
Onde é a viscosidade, é o gradiente de pressão longitudinal e a derivada de segunda ordem da velocidade em relação ao y.
Se nós queremos achar a velocidade só nos resta integrar, não é verdade?
Vamos fazer a primeira derivada:
Colocando na segunda derivada:
Agora nós precisamos usar as condições de contorno para nos ajudar a achar as constantes.
A primeira condição é dada por:
Substituindo na equação:
A segunda condição de contorno que nós conhecemos é:
Quando nós substituímos:
Colocando as constantes na fórmula que descobrimos da velocidade:
O próximo passo aqui é tentar deixar ela mais parecida com a que temos em (a), e vamos começar colocando alguns valores em evidência:
Até aqui tudo bem, mas agora o que temos que fazer é achar a velocidade média para esta equação.
Como? Siimples !!
Basta nós usarmos a fórmula:
Se
Quando nós inserimos esta equação na equação da velocidade ela fica assim:
Igualzinho o que o problema nos disse, certo?
Passo 2
Na letra (b) nós precisamos escrever uma expressão definindo o fator de atrito, f, usando como comprimento característico o diâmetro hidráulico .
Para isso nós vamos lembrar que o fator de atrito pode ser expresso como:
Onde é a queda de pressão através do canal de comprimento L e a densidade.
Mas a letra (b) não pediu só isso, certo? Também nos perguntou qual é o diâmetro hidráulico para o canal de placas paralelas.
O diâmetro hidráulico pode ser dado por:
Onde a área da seção transversal e o perímetro são dados em função das distâncias da placa, , e a largura do canal
Então:
Já que
Passo 3
A letra (c) nos diz que o fator de atrito é estimado como a expressão , e precisamos calcular o coeficiente C!!
Novamente nós vamos lembrar que:
Também já vimos que:
Substituindo:
Lembrando que:
E manipulando um pouco a equação:
Então:
E olha que massaaa !
Portanto:
E consequentemente:
Passo 4
Na letra (d) nós queremos calcular a velocidade média e o número de Reynolds para o ar.
O problema nos disse que:
Para esta temperatura a Tabela A.4 nos diz que, para o ar:
Já sabemos que a velocidade média é dada por:
Substituindo os valores que nós temos:
O número de Reynolds também está fácil:
Substituindo:
Como o número de Reynolds é menor que 2300 o fluxo é laminar, mas não completamente desenvolvido.
Nestes casos o fator de atrito na região de entrada é maior do que para as condições de escoamento completamente desenvolvido, ok?
Se é assim, a velocidade média é menor do que nós estimamos para a mesma queda de pressão!!