Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 25
No escoamento por um tubo de um fluido muito viscoso, a perda de carga é dada por , onde e são os adimensionais obtidos de e , pelo teorema dos , usando as bases entre parênteses, e é o comprimento da tubulação.
Desprezando as perdas de carga singulares, determinar:
- Os adimensionais pelo teorema dos , usando as bases dadas;
- A velocidade teórica do fluido na tubulação;
- A velocidade real do fluido na tubulação;
- O coeficiente de perda de carga distribuída.
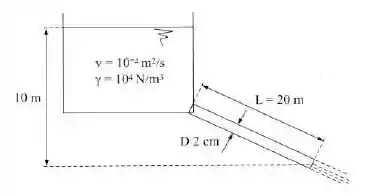
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Sabemos que a vazão é uma função do diâmetro do escoamento e da aceleração da gravidade. Logo:
O que nos leva ao sistema linear:
Portanto:
Então o primeiro adimensional será:
Passo 2
O segundo adimensional será:
Resolvendo o sistema linear, temos que:
Passo 3
A velocidade teórica do escoamento é a velocidade calculada desconsiderando as eventuais perdas de carga no sistema. Sendo assim, podemos utilizar a equação de Bernoulli entre as superfícies do reservatório e a saída do escoamento, considerando que ambos os pontos estão à pressão atmosférica e que o reservatório é de grandes dimensões.
A velocidade real do escoamento é menor que a velocidade teórica. Neste exercício consideramos apenas as perdas por cargas distribuídas:
Resolvendo encontraremos:
A equação de Bernoulli considerando as perdas fica:
Passo 4
Para calcular o fator de atrito, vamos utilizar a expressão da perda de carga distribuída com a velocidade real de escoamento: