Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 35

Considere um coletor solar de ar que tem 1   m de largura e 5   m de comprimento e espaçamento constante de 3   c m entre a tampa de vidro e a chapa do coletor. O ar escoa a uma temperatura média de 45   ° C e taxa de 0,15   m 3 / s através da lateral com 1   m de largura do coletor e ao longo da passagem de   5   m de comprimento. Desprezando os efeitos da entrada e da rugosidade, determine a queda de pressão do coletor.

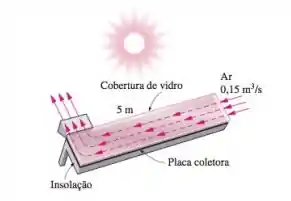
Passo 1

Fala aí galera, bora resolver mais uma questão de Mecânica dos Fluidos. Para determinarmos a queda de pressão do coletor precisamos primeiro encontrar a vazão mássica, a área da seção transversal, o diâmetro hidráulico, a velocidade média e o número de Reynolds.

Sabemos que as propriedades do ar a 1   a t m e 45   ° C são:

ρ = 1,109   k g / m 3

μ = 1,941 × 10 - 5   k g / m ∙ s

v = 1,750

Logo, para a vazão mássica, temos:

m ˙ = p V ˙ m ˙ = ( 1,11   k g / m 3 ) ( 0,15   m 3 / s )

m ˙ = 0,1665   k g / s

Passo 2

Para encontrarmos a seção transversal, temos uma área retangular, logo:

A C = a × b A C = 1 1   m 0,03   m A C = 0,03   m 2

Passo 3

Agora, vamos encontrar o diâmetro hidráulico. Temos:

D h = 4 A c P = 4 ( 0,03   m 2 ) 2 1 + 0,03 m

D h = 0,05825   m

Onde P é o perímetro úmido da seção.

Passo 4

Já para a velocidade média, podemos encontrá-la a partir da relação entre a vazão volumétrica e da seção transversal. Fica assim:

V m é d i a = V ˙ A C = 0,15   m 3 / s 0,03   m 2

V m é d i a = 5   m / s

Passo 5

Em seguida, para obtermos o número de Reynolds temos que:

R e = V D h v R e = ( 5   m / s ) ( 0,05825   m ) 1,750 × 10 - 5   m 2 / s

R e = 1,664 × 10 4

Passo 6

Com isso, podemos concluir que o fluxo é turbulento já que o número de Reynolds R e é maior que 4000 .

O fator de atrito correspondente a este número de Reynolds para uma seção de fluxo suave ( ε / D = 0 ) pode ser obtido a partir da equação de Colebrook, temos:

1 f = - 2,0 log ⁡ ε / D 3,7 + 2,51 R e f

1 f = - 2,0 log ⁡ ( 0 + 2,51 16,640 f

Resolvendo esta expressão vamos encontrar um falor de f de:

f = 0,0271

Passo 7

Por fim, a queda de pressão é dada por:

∆ P = f L D ∙ ρ V 2 2 ∆ P = 0,0271 5   m 0,05825   m ( 1,11   k g / m 3 ) ( 5   m / s ) ² 2

∆ P = 32,3   P a

Resposta

∆ P = 32,3   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na instalação da figura são dados: Q = 4L / s ; área da seção das tubulações A = 20c m 2 ; potência da máquina N M = 0,19k W ; perda de carga distribuída é diretamente proporcional ao comprimento da t
Ao repor o óleo de um motor no posto de serviços,, o frentista mantém o funil sempre constantemente cheio. Como o óleo tem uma elevada viscosidade cinemática ( 10 - 5 m 2 / s ) , supõe-se que o escoam
Para o escoamento laminar na seção de tubo mostrada na Fig. 8.1, trace a tensão de cisalhamento de parede, a pressão e a velocidade na linha de centro como funções da distância ao longo do tubo. Expli
Ar a 40°C escoa em um sistema de tubos em que o diâmetro é reduzido em dois estágios de 25 mm para 15 mm e para 10 mm. Cada seção tem 2 m de comprimento. A medida que a vazão é aumentada, em qual seçã
Analise o escoamento através de uma expansão súbita, aplicando as equações básicas a um volume de controle começando na expansão e terminando a jusante dela (admita que a pressão de entrada p 1 age so