Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 29
O dispositivo da figura gira a , acionado por um motor que mantém o torque constante, independentemente da rotação. Para variar a rotação, deloca-se o mancal móvel para a esquerda. Qual a nova rotação atingida, em , deslocando totalmente o mancal? Dado: .
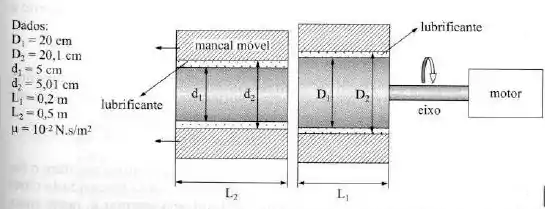
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A área do cilindro é dada por:
O torque do motor é dado por:
E a tensão de cisalhamento é dada pela seguinte expressão:
Considerando uma camada muito fina de fluido, a expressão anterior se torna:
Passo 2
Sendo assim, as áreas serão:
Assim, podemos calcular as tensões de cisalhamento do fluido em cada cilindro:
E:
Passo 3
As forças de cisalhamento tangenciais são dadas por:
E:
O torque total é dado por:
Passo 4
Como temos a velocidade de rotação dada pelo exercício, podemos transformar essa velocidade em velocidades lineares tangenciais a cada cilindro do problema a partir da expressão , logo:
E:
A força de cisalhamento tangencial ao cilindro do primeiro mancal é dada por:
Logo, temos uma nova tensão de cisalhamento na superfície deste cilindro:
Assim podemos obter a velocidade linear do cilindro: