Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 53
Uma esfera oca de alumínio, com um aquecedor elétrico no centro, é usada em testes para determinar a condutividade térmica de materiais isolantes. Os raios interno e externo da esfera são e , respectivamente, e o teste é feito em condições de estado estacionário com a superfície interna do alumínio mantida a . Em um teste particular, uma casca esférica de isolamento é fundida na superfície externa da esfera com uma espessura de . O sistema está em uma sala para a qual a temperatura do ar é de e o coeficiente de convecção na superfície externa do isolamento é de . Se forem dissipados pelo aquecedor em condições de estado estacionário, o que é a condutividade térmica do isolamento?
Passo 1
Fala Pessoal!! Bora fazer essa questão comigo!!
Para resolver essa questão, podemos começar fazendo as seguintes suposições:
(1) Condições de estado estacionário.
(2) Condução radial unidimensional.
(3) Propriedades constantes.
(4) Resistência de contato insignificante.
(5) Troca de radiação insignificante na superfície externa.
Os dados fornecidos foram:
Raio interno da esfera:
Raio externo da esfera:
Espessura do isolamento:
Raio externo:
Temperatura na superfície interna:
Temperatura do ar ambiente:
Coeficiente convectivo na superfície externa do isolamento:
Calor dissipado:
Propriedades:
Pela Tabela A-1 a
Condutividade térmica do Alumínio:
Passo 2
Para resolver essa questão, podemos fazer um circuito térmico que representa a condução de calor no sistema. O circuito tem a seguinte forma:
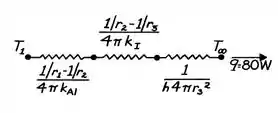
Do circuito térmico, podemos escrever o seguinte:
Como nós queremos a condutividade térmica do isolamento, podemos isolado da seguinte forma:
Substituindo os termos da expressão acima pelos dados fornecidos, temos:
Portanto, a condutividade térmica do isolamento é .