Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 9

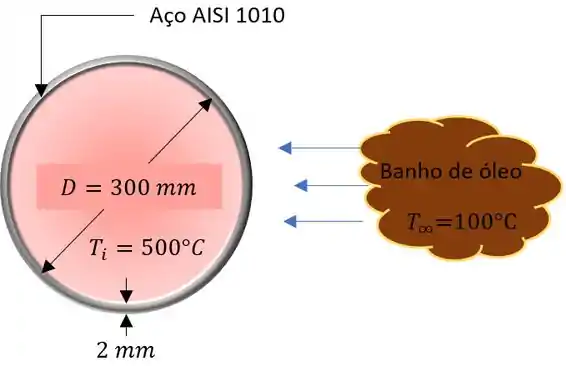
Uma esfera sólida de aço ( A I S I   1010 ) , com diâmetro de 300   m m , é revestida com uma camada de um material dielétrico com espessura de 2   m m e condutividade térmica de 0,04   W / ( m   ·   K ) . A esfera revestida encontra-se inicialmente a uma temperatura uniforme de 500 ° C e é subitamente resfriada pela imersão em um grande banho de óleo, no qual

T ∞ = 100 ° C e h   =   3300   W / ( m 2   ·   K ) . Estime o tempo necessário para a temperatura da esfera revestida atingir 140 ° C . Sugestão: Despreze o efeito do armazenamento de energia no material dielétrico, uma vez que a sua capacitância térmica ( ρ c   V ) é pequena quando comparada à da esfera de aço.

Passo 1

Vamos lá! Nosso problema nos pede a temperatura para chegar a temperatura de 140 ° C .

Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - R e s i s t ê n c i a   p o r   c o n t a t o   d e s p r e z í v e l  

I I I - T e m p e r a t u r a   n a   e s f e r a   r a d i a l m e n t e   c o n s t a n t e

I V - E s p e s s u r a   d a   c a m a d a   d i e l é t r i c a   d e s p r e z í v e l   e m   c o m p a r a ç ã o   a o   r a i o   d a s   e s f e r a

V - C a p a c i a n t a c i a   t e r m i c a   d a   c a m a d a   d i e l é t r i c a   d e s p r e z í v e l

Passo 2

Vamos usar os dados da tabela A - 1 pro Aço AISI 1010.

Agora que fizemos a análise do nosso problema vamos as nossas contas, primeiro vamos calcular a resistência térmica devido a camada dielétrica.

R ' ' = l k + 1 h = 0,002 0,04 + 1 3300 = 0,05 + 0,0003 = 0,0503   m 2 ⋅ K W

A resistência é dada por:

U = 1 R ' ' = 1 0,0503 = 19,88 W m 2 ⋅ K

Agora calculando o número de B i o t pra verificar nossa condição de espacialmente isotérmica, assim temos:

B i = U L c k = U D 6 k = 19,88 ⋅ 0,300 6 ⋅ 48,8 = 0,0204

Como B i < 0,1 a consideração é aceitável!

Passo 3

Agora para encontrarmos o tempo necessário pra chegarmos a temperatura que é solicitada vamos aplicar nossa equação 5.5 usando U , assim temos:

t = ρ c U V A s ln ⁡ θ i θ 0 = ρ c U V A s ln ⁡ T 0 - T ∞ T ∞ - T ∞  

Substituindo V A s = D 6

t = 7.832 k g m 3 ⋅ 559 J k g ⋅ K 19.88 W m 2 ⋅ K ⋅ 0,300   m 6 ⋅ ln ⁡ 500 - 100 ° C 14 0 - 100 ° C    

t = 25.358   s

t = 7,04   h r s

Resposta

t = 7,04   h r s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de Biot durante um processo de transferência de calor entre a esfera e seus arredores é 0,02 . Você usaria a análise de sistemas aglomerados ou gráficos de temperatura transiente para determi
Qual é o significado físico do número de Fourier? O número de Fourier de determinado problema de transferência de calor dobra quando o tempo é duplicado?
Um ovo deve ser cozido em água fervente. O tempo de cozimento pode ser encurtado com aumento da taxa de calor para tornar a ebulição da água mais rápida?
Um corpo com temperatura inicial T i é colocado em um meio a uma temperatura constante T ∞ . Como determinar a quantidade máxima possível de transferência de calor entre o corpo e o meio envolvente?
Molas em um sistema de suspenção de automóveis são barras de aço aquecidas que, enquanto estão maleáveis, são enroladas em bobinas. Considere barras de aço ρ = 7.832k g / m 3 , c p = 434J / k g ⋅ K ,