Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 11

A placa base de um ferro de passar tem uma espessura de L   =   7   m m   e é feita com uma liga de alumínio ρ   =   2800 k g m 3 ,   c   =   900 J k g   ·   K ,   k   =   180 W m   ·   K ,   ε   =   0,80 . Um aquecedor de resistência elétrica é fixado à superfície interna da placa, enquanto a superfície externa é exposta ao ar ambiente e a uma grande vizinhança a T ∞   =   T v i z   =   25 ° C . As áreas das superfícies interna e externa são cada uma A s   =   0,040   m 2 .

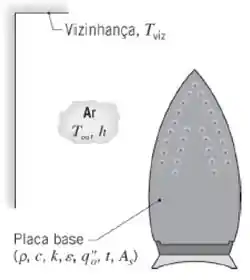
Se um fluxo térmico aproximadamente uniforme de q 0 ' ' =   1,25   ×   104   W / m 2   for aplicado na superfície interna da placa base do ferro e o coeficiente convectivo na superfície externa for h = 10 W m 2   ·   K , estime o tempo necessário para a placa atingir uma temperatura de 135 ° C . Sugestão: Integração numérica é sugerida para resolver o problema.

Passo 1

Vamos lá! Nosso problema nos pede o tempo necessário para a placa do ferro atingir 13 5   ° C , mas antes que tal desenharmos o comportamento desse problema pra entendermos o que o ocorre. Fica assim.

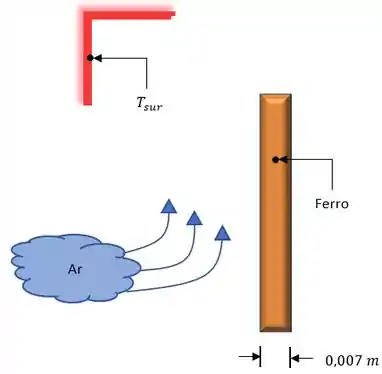
Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - T r a n s f e r e n c i a   e n t r e   u m a   p e q u e n a   s u p e r f i c i e   e   e n v o l t o   e m   u m   m e i o   g r a n d e  

I I I - C o e f i c i e n t e   d e   c o n v e c ç ã o   c o n s t a n t e   i n d e p e n d e n t e   d o   t e m p o

I V - I n i c i a l m e n t e   o   f e r r o   e s t á   e m   t e m p e r a t u r a   a m b i e n t e

Passo 2

Agora vamos calcular o número de B i o t pra verificar nossa condição de espacialmente isotérmica, mas antes devemos lembrar que o número de B i o t se trata tanto para o coeficiente de convecção tanto pro coeficiente convectivo pra radiação, assim pra calcularmos o coeficiente de convecção por radiação temos que usar a equação 1.9 .

h r = ε σ T + T s u r T 2 + T s u r 2

0,8 ⋅ 5,67 ⋅ 10 - 8 408 + 298 408 2 + 298 2 = 8,2   W m 2 ⋅ K

Calculando agora nosso número de B i o t temos:

B i = h L c k = 10 W m 2 ⋅ K ⋅ 7,0 ⋅ 10 - 3 m 180   W m ⋅ K = 3,9 ⋅ 10 - 4

B i r = h r L c k = 8,2 W m 2 ⋅ K ⋅ 7,0 ⋅ 10 - 3 m 180   W m ⋅ K = 3 , 2 ⋅ 10 - 4

Como B i , B i r , B i + B i r ≪ 0,1 a consideração de concentração da capacitância é aceitável!

Passo 3

Agora para encontrarmos o tempo necessário pra chegarmos à temperatura que é solicitada vamos aplicar nossa equação 5 . 1 5 , assim temos:

T - T i = A s ρ V c ∫ 0 t q h ' ' - h T - T ∞ - ε σ T 4 - T ∞ 4 d t

Integrando chegamos à:

t = T - T i ρ V c A s q h ' ' - h T - T ∞ - ε σ T 4 - T ∞ 4

Para T = 135   ° C .

t = 168   s

Isso é tudo pessoal!

Resposta

t = 168   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tarugo de madeira cilíndrico ( k = 0,17W / m ⋅ Keα = 1,28 × 10 - 7m 2 / s ) tem 10c m de diâmetro e está inicialmente na temperatura uniforme de 25 ℃ ℃. É exposto a gases quentes a 600 ℃ ℃ na larei
Um dispositivo eletrônico dissipando 18W tem massa de 18g , calor específico de 850J / k g ⋅ K e área de 4c m 2 . O dispositivo é usado levemente, ficando ligado por 5 minutos e depois desligado por v
Um tijolo de dimensão 203 × 102 × 57m m é queimado em um forno a 1.100 ℃ ℃ e depois resfriado em uma sala à temperatura ambiente de 30 ℃ ℃ com coeficiente de transferência de calor de convecção de 5W
Bolas de aço de carbono ρ = 7.833k g / m 3 ,k = 54W / m ⋅ K ,c p = 0,465k J / k g ⋅ Keα = 1,474 × 10 - 6m 2 / s de 8m m de diâmetro são recozidos por aquecimento a 900 ℃ ℃ em forno e, depois, esfriado
Barras de aço ( ρ = 7.832k g / m 3 ,c p = 434J / k g ⋅ Kek = 63,9W / m ⋅ K ) são aquecidas em um forno a 850 ℃ ℃ e depois mergulhadas em banho-maria a 50 ℃ ℃ por um período de 40 segundos como parte d