Um espaço fechado vertical de 1,5 m de altura e 3,0 m de largura consiste de duas superfícies separadas por um espaçamento de 0,4 m de ar à pressão atmosférica. Considerando que as temperaturas das superfícies através do espaçamento de ar são 280 K e 336 K e as emissividades são 0,15 e 0,90, determine a fração de calor transferida através do espaço fechado por radiação.
Passo 1
Shoow galerinha!!
Nós temos algo parecido com este desenho aqui:
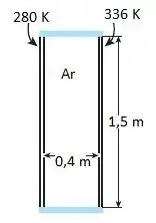
Nós teremos duas formas de calor atuando aqui, a convectiva e a radioativa:
Então, para acharmos a fração desse calor que é transferido por meio de radiação nós precisaremos achar as três formas de calor, ok?
Vamos começar pela convectiva:
Como estamos trabalhando com um espaço retangular:
Então:
Já temos algumas informações certo?
A única coisa que precisamos é o coeficiente convectivo!
Bora calculá-lo?
Passo 2
Bom galera, o coeficiente convectivo é dado por:
Sabemos que:
Para achar os demais nós vamos precisar da temperatura média:
Em graus Celsius:
Com isso já conseguimos calcular o coeficiente de expansão volumétrica:
E olhando as demais propriedades na Tabela A-15:
Com isso tudo nós já conseguimos calcular o número de Rayleigh:
Substituindo:
Como , podemos calcular o número de Nusselt como:
Substituindo nossos dados:
Agora sim nós conseguimos calcular o coeficiente convectivo:
Passo 3
Com todos os dados nós conseguimos calcular a transferência de calor por convecção:
Com isso nós podemos começar a calcular a transferência de calor com radiação:
A área neste caso é igual:
Como a constante de Boltzmann é tabelada:
Só nos falta achar a emissividade efetiva, não é?
Passo 4
Para calcular a emissividade efetiva vamos usar uma fórmula:
Lembrando que:
Então:
Calculando o calor convectivo:
Passo 5
Com todas as transferências de calor encontradas nós podemos calcular a transferência total:
Ufaaa!!
Acabou?
Claaaro que não kkkkk
Ainda precisamos da fração de calor transferida através do espaço fechado por radiação:
Gostaram dessa ?!