Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 65

Duas esferas concêntricas com diâmetros de 5 cm e 10 cm têm as temperaturas da superfície mantidas em 100°C e 200°C, respectivamente. O espaço entre as duas superfícies esféricas é preenchido com gás nitrogênio a 1 atm. Determine a taxa de transferência de calor através do espaço entre as duas superfícies esféricas.

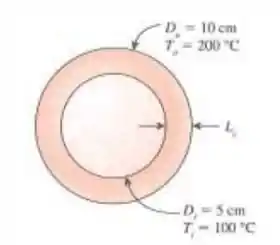
Passo 1

Bora continuar !!

Então galera, a taxa de transferência de calor para o espaço delimitados por duas superfícies esféricas é dado por:

Q ˙ = k e f e t i v o π D i D 0 L c ( T 0 - T i )

Até agora nós sabemos que:

D i = 5   c m = 0,05   m

D 0 = 10   c = 0,1   m

T 0 = 200 ° C

T i = 100 ° C

O comprimento característico nós não temos, mas calcular ele é molezinha:

L c = D 0 - D i 2 = 0,1   m - 0,05   m 2

L c = 0,0 25   m

A única coisa que nós não temos é a condutividade efetiva, mas vamos calcular!!

Passo 2

Para espaços esféricos o valor da condutividade efetiva é calculado segundo a fórmula:

k e f e t i v o = 0,74 k P r 0,861 + P r 1 4 F e s f R a 1 4

Antes de qualquer coisa vamos obter as propriedades do nitrogênio na sua temperatura média:

T m é d i a = T 0 + T i 2 = 200 ° C + 100 ° C 2 = 150 ° C

Com isso já conseguimos calcular o coeficiente de expansão volumétrica:

β = 1 T m é d i a = 1 150 + 273   K = 0,002364   K - 1  

E olhando as demais propriedades na Tabela A-16:

k = 0,0 3416 W m . ° C

P r = 0,7 025

v = 2,851 × 10 - 5 m 2 s

Com isso tudo nós já conseguimos calcular o número de Rayleigh:

R a = g β T 0 - T i L c ³ v 2 P r

Substituindo:

R a = 9,81 m s 2 0,002364   K - 1 200 ° C - 100 ° C 0,025 3 2,851 × 10 - 5 m 2 s 2 0,7025

R a = 3,13 17 × 10 4

Passo 3

O próximo passo é calcularmos o fator geométrico para esferas concêntricas:

F e s f = L c D i D 0 4 D i - 7 5 + D 0 - 7 5 5

Substituindo os dados que já temos:

F e s f = 0,025   m 0,05   m × 0,1 m 4 0,05   m - 7 5 + 0 , 1   m - 7 5 5

F e s f = 6,2682 × 10 - 3

Agora nós podemos calcular a condutividade térmica efetiva:

k e f e t i v o = 0,74 0,03416 W m . ° C 0,7025 0,861 + 0,7025 1 4 6,2682 × 10 - 3 × 3,1317 × 10 4 1 4

k e f e t i v o = 0,07747   W m . ° C

Passo 4

Agora nós temos tudo o que precisamos para calcular a transferência de calor:

Q ˙ = 0,07747   W m . ° C π × 0,05   m × 0,1   m 0,0 2 5   m ( 200 ° C - 100 ° C )

Q ˙ = 4,867   W

E assim nós finalizamos mais umaa !!

Resposta

Q ˙ = 4,867   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um azulejo quadrado, com 200m m de lado e 10m m de espessura, tem as propriedades termo físicas do Pyrex ( ε = 0,80 ) e sai de um processo de cura a uma temperatura inicial de T i = 140 ° C . A superf
Uma longa linha de vapor não isolada, na posição horizontal, com 100m m de diâmetro externo e uma emissividade de 0,8 , transporta vapor a 200°C e está exposta ao ar atmosférico e a uma grande vizinha
Uma janela de vidro duplo, vertical, que tem 1m de lado e um espaço de 25m m preenchido com ar atmosférico, separa o ar quiescente de uma sala a T ∞ , i = 20 ° C do ar ambiente externo, também quiesce
A parede plana unidimensional da Figura 3.1 tem espessura L=75m m e condutividade térmica k = 2 , 5W / ( m·K ) . As temperaturas do fluido são T ∞ , 1 =200 ° C e T ∞ , 2=100 ° C , respectivamente. Usa
Considere um objeto com comprimento característico de 0,01 5m e uma situação na qual a diferença de temperaturas é de 1 0° C . Estimando as propriedades termofísicas nas condições especificadas, deter