Módulos termoelétricos têm sido utilizados para gerar potência elétrica através do aproveitamento do calor gerado em fogões a lenha. Considere a instalação de um módulo termoelétrico do Exemplo 3.13 em uma superfície vertical de um fogão a lenha que tem uma temperatura superficial de . Uma resistência térmica de contato de está presente na interface entre o fogão e o módulo termoelétrico, enquanto o ar da sala e suas paredes encontram-se a . A superfície exposta do módulo termoelétrico tem uma emissividade e está submetida a um coeficiente convectivo . Esboce o circuito térmico equivalente e determine a potência elétrica gerada pelo módulo. A resistência elétrica da carga é de .
Passo 1
Fala aí! Vamos resolver essa questão? Partiu!
Ela pede pra gente esboçar o circuito e depois determinar a potência elétrica gerada, show?
Vamos nessa!
O nosso circuito vai ficar com essa cara aqui olha:
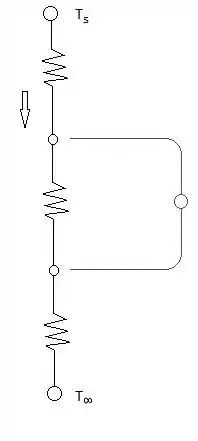
Agora vamos lembrar que pra calcular nossa potência podemos usar a fórmula:
Passo 2
Vamos então encontrar esse , beleza? Pra isso precisamos do:
Agora precisaremos usar as equações 3.125 e 3.126 do livro… Tudo em prol da corrente, vamos lá:
Vamos tentar encontrar o :
Opa! Precisamos desse , vamos achar ele assim:
Agora podemos voltar na equação ali de cima:
Agora vamos encontrar o nosso :
O também é uma função de , então vamos substituí-lo:
Se a nossa energia produzida é igual a nossa energia dissipada, vamos ter que:
Passo 3
Agora podemos montar o que achamos em um sistema de três equações e três incógnitas, olha só:
Sistema a gente já está acostumado a resolver, né? Apesar deste ser mais complexo, a gente consegue tranquilo… E resolvendo esse carinha aí vamos ter que:
Agora é só retornar lá na nossa equação da potência:
Conseguimos!