Estime o nível mínimo de água no tanque do Problema 8.115 de modo que o escoamento seja ainda turbulento.
Passo 1
Oi pessoal, tudo bem ?
Bem, vamos relembrar os dados do problema 8.115:
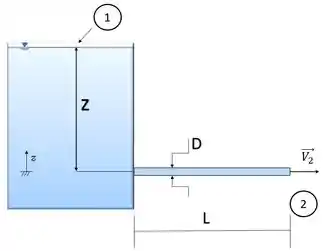
| | |
E, de acordo com o Apêndice A:
|
Passo 2
Como se pode perceber:
Como o tanque 1 é muito grande, considera-se a velocidade nula,
O referencial da altura se inicia no duto 2, portanto
Relembrando a equação da perda de carga:
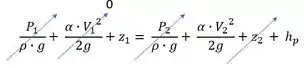
Segundo o autor, a perda de carga é dada pela soma da perda de carga menor com a menor, então:
Reescrevendo a equação da perda de carga:
Porém, como o problema deseja que o escoamento seja turbulento, o fator de atrito se faz de forma diferente de quando o escoamento é laminar. Então:
)
Passo 3
Sabendo que, do problema 8.115:
Re utilizado e V calculado
Utilizando a ferramenta Solve, do excel, é possível estimar o valor do coeficiente de atrito f.
O fator de atrito recebe o valor de 0,0473 (turbulento)
E a profundidade Z recebe o valor de 6,13 m.
Resposta
Portanto, o nível mínimo de água no tanque deve ter uma profundidade de Z=6,13m para que o escoamento ainda seja turbulento.