Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 23
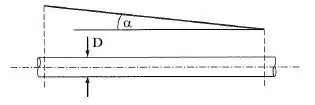
Água escoa em regime laminar num conduto cilíndrico horizontal de diâmetro D. A linha de energia forma com a horizontal um ângulo . Determinar a vazão. Dados: ; ; ; .
Passo 1
Conforme sabemos, quando temos a linha de energia formando um certo ângulo com a horizontal e não temos perdas localizadas nesse trecho, então podemos escrever a perda de carga distribuída em função desse ângulo:
Abrindo a expressão, temos:
Passo 2
No entanto, o enunciado nos disse que o escoamento é laminar, e através da equação 7.11, apresentada nessa seção, podemos encontrar :
Substituindo essa expressão na última equação do passo 2, temos:
Isolando da expressão e substituindo os valores conhecidos, temos:
Passo 3
Agora podemos usar a velocidade para encontrar a vazão no sistema:
Resposta
Exercícios de Livros Relacionados
Ar na condição padrão escoa através de uma expansão súbita em um duto circular. Os diâmetros do duto a montante e a jusante da expansão são 75 mm e 225 mm, respectivamente. A pressão a jusante é 5 mm
O diagrama de Moody dá o fator de atrito de Darcy, f , em termos do número de Reynolds e da rugosidade relativa. O fator de atrito de Fanning para escoamento em tubo é definido como: f F = τ w 1 2 ρ V
Água escoa através de um tubo de 50 mm de diâmetro que subitamente contrai-se para 25 mm. A queda de pressão através da contração é 3,45 kPa. Determine a vazão volumétrica.
Água escoa a 25 L/s através de uma constrição suave, em que o diâmetro do tubo é reduzido de 75 mm para 37,5 mm, segundo um ângulo de 150°. Se a pressão antes da constrição for 500 kPa, estime a press
Ar escoa para fora de uma câmara de teste de uma sala limpa através de um duto de 150 mm de diâmetro e de comprimento L. O duto original tinha uma entrada de borda-viva, mas essa foi substituída por o