Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 19

No estudo analítico de um furacão, admitiu-se que o escoamento resulte da superposição de um vórtice ideal com um sorvedouro no ponto O. Sendo a função potencial do sorvedouro ϕ = - q 2 π ln ⁡ r   e a função ideal de corrente do vórtice ideal Ψ = - Γ 2 π ln ⁡ r   onde q = 2 ⋅ 10 4 m 3 s ⋅ m   e Γ = 5 ⋅ 10 4 m 2 s , determinar:

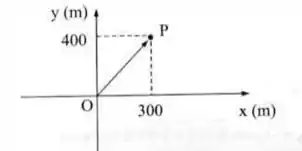
  1. A velocidade do escoamento no ponto P dado por x p = 300   m e y p = 400   m ;
  2. O lugar geométrico dos pontos de mesma pressão que passa por P.

Sabe-se que ao longe p = p 0 e v = v 0 constantes.

Passo 1

Item A)

Agora podemos utilizar a 11.33 temos:

v r = ∂ Ψ r ∂ θ     e     v θ = - ∂ Ψ ∂ r

Perceba que não podemos encontrar v r facilmente, já que Ψ não é explicitamente derivável em θ . Mas pelas equações 11.33 temos:

∂ Ψ r ∂ θ = ∂ ϕ ∂ r

∂ Ψ r ∂ θ = ∂ - q 2 π ln ⁡ r   ∂ r

∂ Ψ = - q 2 π ⋅ 1 r r ∂ θ

Ψ = - q 2 π θ

Agora podemos utilizar a 11.33 temos:

v r = ∂ Ψ r ∂ θ ⇒ v r = ∂ r ∂ θ - q 2 π θ ⇒ v r = - q 2 π r  

v θ = - ∂ Ψ ∂ r ⇒ v θ = - ∂ - Γ 2 π ln ⁡ r   ∂ r ⇒ v θ = Γ 2 π ⋅ 1 r

Passo 2

As nossas equações estão em coordenadas polares, e o ponto P em coordenadas cartesianas. Mas utilizando estas coordenas podemos encontrar o raio:

r = x p 2 + y p 2 = 300 2 + 400 2 ⇒ r = 500   m

Então:

v r = - q 2 π r = 2 ⋅ 10 4 2 π ⋅ 500 ⇒ v r = - 20 π m s

v θ = Γ 2 π ⋅ 1 r = 5 ⋅ 10 4 2 π ⋅ 500 ⇒ v θ = 50 π m s

Expressando vetorialmente, a velocidade no ponto P é:

v → = - 20 π e → r + 50 π e → θ

Passo 3

Item B)

Em um ponto ao longe, a velocidade é igual ao seu módulo:

v → = - q 2 π r e → r + Γ 2 π ⋅ 1 r e → θ

v → = v 0 = - q 2 π r 2 + Γ 2 π ⋅ 1 r 2

v 0 = 1 2 π r q 2 + Γ 2

Agora, isolando o raio:

r = 1 2 π v 0 q 2 + Γ 2

Resposta

  1. v → = - 20 π e → r + 50 π e → θ
  2. r = 1 2 π v 0 q 2 + Γ 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento axissimétrico permanente incompressível ( r ,z ) e u r ,u z para o qual a função corrente é definida por u r = - 1 r ∂ ψ ∂ z e u z = 1 r ∂ ψ ∂ r . Verifique se ψ assim definida
Se a velocidade média no ramo principal do duto do Problema 9-53 for 11,4m / s , calcule a altura h do duto em c m . Obtenha o seu resultado de duas maneiras, mostrando todo o seu trabalho. Você pode
Repita o Problema 9-56 para o caso de uma linha de sumidouros em lugar de uma linha de fontes. Suponha que V ˙ / L seja um valor positivo, mas o escoamento em todos os pontos é na direção oposta.
Considere o escoamento bidimensional permanente, incompressível devido a uma linha de fontes na origem (Figura P9-56). O fluido é criado na origem e se espalha rapidamente em todas as direções no plan
O que é significativo nas curvas com função corrente constante? Explique por que a função corrente é útil na mecânica dos fluidos.