Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 15

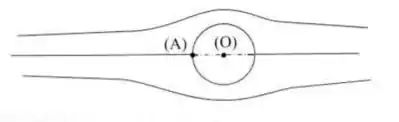
Seja um meteorito que penetra na atmosfera. Admitir em primeira aproximação que o escoamento seja bidimensional e irrotacional na região próxima ao ponto de estagnação. Sabe-se que o escoamento pode ser representado pela superposição de uma fonte de intensidade q , com origem em (O), com um escoamento uniforme de velocidade v 0 na direção mostrada na figura.

  1. Determinar as expressões das funções potencial e de corrente correspondentes à superposição, em coordenadas polares.
  2. Determinar a expressão das componentes da velocidade em função de v 0 ,   q ,   θ ,   r .
  3. Se v 0 = 1000   m / s e o corpo tem raio de 1 m, determinar a intensidade da fonte para que se tenha o escoamento desejado.

Passo 1

Uma fonte (1) pode ser descrita pelas equações da página 306 do livro:

ϕ 1 = q 2 π ln ⁡ r

Ψ 1 = q 2 π θ

E o escoamento em coordenadas polares (2) pode ser descrito pelas equações:

ϕ 2 = v 0 r cos ⁡ θ

Ψ 2 = v 0 r sen ⁡ θ

Passo 2

Item A)

A superposição das expressões da cora das linhas de corrente é:

Ψ = Ψ 2 + Ψ 1

Ψ = q 2 π θ + v 0 r sen ⁡ θ

E a superposição das funções potenciais:

ϕ = ϕ 1 + ϕ 2

ϕ = q 2 π ln ⁡ r + v 0 r cos ⁡ θ

Passo 3

Item B)

As componentes de velocidade podem ser encontradas pelas equações 11.33

v r = ∂ ϕ ∂ r   e   v θ = ∂ ϕ r ⋅ ∂ θ

Calculando a velocidade no sentido e → r

v r = ∂ ϕ ∂ r

v r = ∂ ∂ r q 2 π ln ⁡ r + v 0 r cos ⁡ θ

v r = q 2 π ⋅ r + v 0 ⋅ cos ⁡ θ

Calculando a velocidade no sentido e → θ

v θ = ∂ ϕ r ⋅ ∂ r

v θ = 1 r ∂ ∂ θ q 2 π ln ⁡ r + v 0 r cos ⁡ θ

v θ = 1 r ⋅ 0 - v 0 r sen ⁡ θ

v θ = v 0 sen ⁡ θ

Passo 4

Item C)

Basta aplicar os valores na equação. Vamos aplicar no ponto A onde v r A = 0 ,   r A = 1   m ,   θ A = π

v r = q 2 π ⋅ r + v 0 ⋅ cos ⁡ θ

0 = q 2 π ⋅ 1 + 1000 ⋅ cos ⁡ π

0 = q 2 π ⋅ 1 - 1000

q = 2000 π m 3 s ⋅ m

Resposta

  1. Ψ = q 2 π θ + v 0 r sen ⁡ θ   ϕ = q 2 π ln ⁡ r + v 0 r cos ⁡ θ
  2. v r = q 2 π ⋅ r + v 0 ⋅ cos ⁡ θ

    3. v θ = v 0 sen ⁡ θ

  3. q = 2000 π m 3 s ⋅ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento bidimensional no plano x y .Qual é o significado da diferença do valor da função corrente Ψ de uma linha de corrente para outra?
Considere o campo de velocidade pemanente, bidimensionaldado por V → =u ,v =1,3+2,8 x i →+1,5—2,8 y j → . Verifique se esse campo de escoamento é incompressível.
Imagine escoamento incompressível, permanente, bidimensional que é puramente circular no plano x y ou r θ . Em outras palavras, a componente de velocidade u θ é diferente de zero, mas u r é zero era t
Que restrições ou condições são impostas na função corrente Ψ de maneira que ela satisfaça exatamente a equação da continuidade bidimensional incompressível por definição? Porque essas restrições são
Considere o seguinte campo de velocidade permanente, tridimensional em coordenadas cartesianas: V →=( u ,v ,w )=a x y 2—b i →+c y 3 j →+d x y k → , onde a, b,c ,ed são constantes. Sob que condições es