No Exemplo 8.10, verificamos que a vazão no distribuidor principal de água seria aumentada (algo em torno de 33%) pelo acoplamento de um difusor na saída do bocal instalado nesse distribuidor. Vimos que o comissário de águas Romano exigia que o tubo conectado ao bocal de cada derivação para o consumidor tivesse o mesmo diâmetro por uma distância mínima de 15 m, medida a partir do distribuidor principal. Teria sido o comissário por demais conservador? Usando os dados do problema, estime o comprimento de tubo (com ) para o qual o sistema de tubo e difusor daria uma vazão igual àquela com o bocal apenas. Trace um gráfico da razão de vazões volumétricas como uma função de , em que L é o comprimento do tubo entre o bocal e o difusor, é a vazão para o bocal apenas e Q é a vazão real com o tubo inserido entre o bocal e o difusor.
Passo 1
Oi pessoal, tudo bem ?
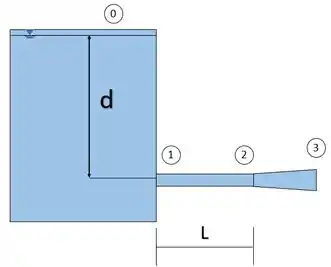
Temos um esboço do problema em questão, em que o difusor encontra-se na extremidade direita.
Bem, para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:
Consideremos:
;
.
As perdas de carga serão representadas pela eq da perda de carga maior e a eq perda de carga menor, de acordo com o exemplo 8.10 , então:
Passo 2
Do problema, temos:
Obs: propriedades da água à , Tabela A.7.
Portanto, a equação de energia simplificada se torna:
Por continuidade:
Então:
Observando o exemplo 8.10 do livro, é possível simplificar a equação:
Como já foi encontrado anteriormente, temos ;
A partir daí, podemos encontrar o valor do Número de Reynolds, sabe-se também que o Re é dado por:
Agora, a partir do Re, podemos encontrar o coeficiente de atrito f.
A equação pode ser resolvida computacionalmente, então, utilizando a ferramenta Solve, do excel, podemos encontrar o valor do fator de atrito .
Passo 3
Substituindo os valores na equação da energia:
Então:
Sabendo disso, perceba que:
Utilizando o excel, é possível incrementar uma tabela em que os valores dos principais parâmentros sejam interdependentes, como na tabela abaixo, com base nas fórmulas e valores já destacados no início da resolução:
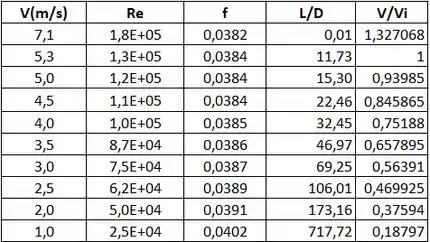
Resposta
Portanto, o gráfico pode ser representado pelo gráfico :
