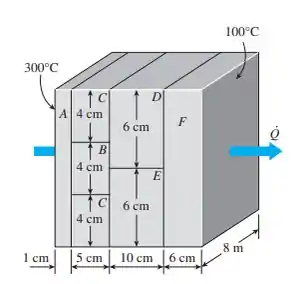
Considere uma parede com 5 m de altura, 8 m de comprimento e 0,22 m de espessura, cuja seção transversal representativa é a fornecida na figura. As condutividades térmicas dos vários materiais utilizados, em , são . As superfícies esquerda e direita da parede são mantidas em temperaturas uniformes de 300°C e 100°C, respectivamente. Supondo que a transferência de calor através da parede seja unidimensional, determine:

1. A taxa de transferência de calor através da parede;
2. A temperatura no ponto em que as seções B, D e E se encontram;
3. A queda de temperatura na seção F. Desconsidere qualquer resistência de contato nas interfaces.

Mais uma que dá medo até de olhar, mas com calma nós vamos!

Começamos como sempre desenhando:

Na letra a nós vamos precisar de todas as resistências:

Para calcularmos cada uma vamos precisar das suas áreas. Fácil, não é?

Só olharmos na figura a altura e considerarmos um comprimento representativo de 1m:

Lançando os dados:

Sabemos que duas placas de C e uma de B estão em paralelo entre si, assim como uma de D e E, certo?

Isolando e substituindo:

E agora eles estão em série com as demais, né?

Para a taxa de calor nós já estamos carecas de saber como calcular, né verdade?

Substituindo:

Como a variação em graus Celsius é a mesma que a variação em kelvin:

Com relação à área representativa:

Como a cada intervalo de a estrutura da parede se repete, para a parede total de 8 m de comprimento e 5 m de altura a troca total de calor será:

Agora vamos para a letra b !!