Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 57

Nitrogênio entra em um bocal convergente-divergente a 700   k P a e 400   K com velocidade desprezível. Determine a velocidade crítica, a pressão, temperatura e massa específica no bocal.

Passo 1

Essa é uma questão sobre escoamento isentrópico (escoamento com entropia constante) de gás ideal (nitrogênio) através de um bocal convergente-divergente. A questão pede quatro coisas diferentes.

A figura abaixo mostra os termos que a questão pede. Cada termo é explicado na lista do que precisa ser calculado nessa questão.

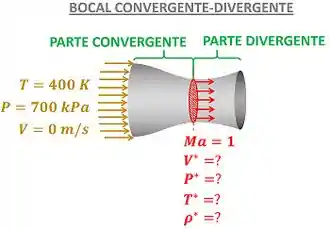
  1. Primeiro, a questão pede para calcular quanto vale a temperatura do nitrogênio quando o número de Mach M a vale 1 M a = 1 . Essa temperatura é chamada de temperatura crítica e é identificada por um asterisco * acima dela.

    2. M a = 1     ⟹     T = T *   t e m p e r a t u r a   c r í t i c a

    Achamos essa temperatura, multiplicando duas equações. Uma equação relaciona a temperatura de entrada T com a temperatura de estagnação do ar T 0 (equação 12-18 do livro).

    T 0 T = 1 + k - 1 2 M a 2

    k é a razão de calroes específicos do gás k = c p / c v que vale 1,4 para o nitrogênio.

    A outra equação relaciona a temperatura de estagnação T 0 com a temperatura crítica T * (equação 12-21 do livro).

    T * T 0 = 2 k + 1

  2. Em segundo lugar, a questão pede para calcular quanto vale a velocidade do nitrogênio quando o número de Mach M a vale 1 M a = 1 . Essa velocidade é chamada de velocidade crítica e é identificada por um asterisco * acima dela.

    3. M a = 1     ⟹     V = V *   v e l o c i d a d e   c r í t i c a

    Achamos essa velocidade usando a equação do número de Mach e a fórmula de velocidade do som para gases ideais.

    M a = V * c *

    onde c * é a velocidade do som, quando M a = 1 .

    c = k R T *

    onde R é a constante do gás que vale 296,8   J / k g K

  3. Em terceiro lugar, a questão pede para calcular quanto vale a pressão do nitrogênio quando o número de Mach M a vale 1 M a = 1 . Essa pressão é chamada de pressão crítica e é identificada por um asterisco * acima dela.

    4. M a = 1     ⟹     P = P *   p r e s s ã o   c r í t i c a

    Achamos P * , multiplicando duas equações. Uma equação relaciona a pressão de entrada P com a pressão de estagnação do ar P 0 (equação 12-19 do livro).

    P 0 P = 1 + k - 1 2 M a 2 k k - 1

    A outra equação relaciona a pressão de estagnação P 0 com a pressão crítica P * (equação 12-22 do livro).

    P * P 0 = 2 k + 1 k k - 1

  4. Em quarto lugar, a questão pede para calcular quanto vale a densidade do nitrogênio quando o número de Mach M a vale 1 M a = 1 . Essa densidade é chamada de densidade crítica e é identificada por um asterisco * acima dela.

M a = 1     ⟹     ρ = ρ *   d e n s i d a d e   c r í t i c a

Achamos ρ * , multiplicando duas equações. Uma equação relaciona a densidade de entrada ρ com a densidade de estagnação do ar ρ 0 (equação 12-20 do livro).

ρ 0 ρ = 1 + k - 1 2 M a 2 1 k - 1

A outra equação relaciona a densidade de estagnação ρ 0 com a densidade crítica ρ * (equação 12-23 do livro).

ρ * ρ 0 = 2 k + 1 1 k - 1

A densidade de entrada ρ é encontrada através da equação de gás ideal abaixo.

ρ = P R T

Passo 2

Nesse passo, resolveremos o primeiro tópico que a questão quer saber: quanto vale T * . Pra isso, vamos multiplicar as duas equações que mencionamos. Isso é feito para cortar a temperatura de estagnação T 0 da equação

T 0 T ⋅ T * T 0 = 2 k + 1 ⋅ 1 + k - 1 2 M a 2

T * T = 2 k + 1 ⋅ 1 + k - 1 2 M a 2

T * = T ⋅ 2 k + 1 ⋅ 1 + k - 1 2 M a 2

O número de Mach M a dessa fórmula é o número de Mach da entrada do bocal. Ele pode ser calculado através da equação abaixo, lembrando que a velocidade de entrada V vale zero.

M a = V c     ⟹     M a = 0 c     ⟹     M a = 0

Substituindo os dados na equação acima, achamos:

T * = 400 ⋅ 2 1,4 + 1 ⋅ 1 + 1,4 - 1 2 ⋅ 0 2       ⟹       T * = 333 , 3   K

Passo 3

Nesse passo, resolveremos o segundo tópico que a questão quer saber: quanto vale V * . Para Para isso, subsituimos a expressão de c * na equação do número de Mach.

M a = V * c *     ⟹     M a = V * k R T *     ⟹     V * = M a ⋅ k R T *

onde o número de Mach M a dessa fórmula vale 1 .

Substituindo os dados nessa equação, achamos V * .

V * = M a ⋅ k R T *     ⟹     V * = 1 ⋅ 1,4 ⋅ 296,8 ⋅ 333 , 3     ⟹     V * = 372 , 1   m / s

Passo 4

Nesse passo, resolveremos o terceiro tópico que a questão quer saber: quanto vale P * . Pra isso, vamos multiplicar as duas equações que mencionamos. Isso é feito para cortar a pressão de estagnação P 0 da equação

P 0 P ⋅ P * P 0 = 2 k + 1 k k - 1 ⋅ 1 + k - 1 2 M a 2 k k - 1

P * P = 2 k + 1 k k - 1 ⋅ 1 + k - 1 2 M a 2 k k - 1

P * = P ⋅ 2 k + 1 k k - 1 ⋅ 1 + k - 1 2 M a 2 k k - 1

Usando esse valor na fórmula de P * , achamos:

P * = P ⋅ 2 k + 1 k k - 1 ⋅ 1 + k - 1 2 M a 2 k k - 1

P * = 700 ⋅ 2 1,4 + 1 1,4 1,4 - 1 ⋅ 1 + 1,4 - 1 2 ⋅ 0 2 1,4 1,4 - 1       ⟹       P * = 369,8   k P a

Passo 5

Nesse passo, resolveremos o terceiro tópico que a questão quer saber: quanto vale ρ * .

Antes, temos que achar quanto vale a densidade ρ na entrada o bocal. A pressão P deve, primeiro ser convertida de k P a P = 700   k P a para P a P = 700000   P a .

ρ = P R T     ⟹     ρ = 700000 296,8 ⋅ 400     ⟹     ρ = 5,90   k g / m 3

Por fim, multiplicamos as duas equações que mencionamos. Isso é feito para cortar a densidade de estagnação ρ 0 da equação.

ρ 0 ρ ⋅ ρ * ρ 0 = 2 k + 1 1 k - 1 ⋅ 1 + k - 1 2 M a 2 1 k - 1

ρ * ρ = 2 k + 1 1 k - 1 ⋅ 1 + k - 1 2 M a 2 1 k - 1

ρ * = ρ ⋅ 2 k + 1 1 k - 1 ⋅ 1 + k - 1 2 M a 2 1 k - 1

Usando esse valor na fórmula de ρ * , achamos:

ρ * = 5,90 ⋅ 2 1,4 + 1 1 1,4 - 1 ⋅ 1 + 1,4 - 1 2 ⋅ 0 2 1 1,4 - 1       ⟹       ρ * = 3 , 74   k g / m 3

Resposta

T * = 333 , 3   K

V * = 372 , 1   m / s

P * = 369,8   k P a

ρ * = 3 , 74   k g / m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-98 Repita o Problema 13-97 para uma profundidade de escoamento a montante de 1,2 m.
Água deve ser liberada de um lago com 6 m de profundidade em um canal através de uma comporta basculante com uma abertura de 5 m de largura e 0,6 m de altura no fundo. Se aprofundidade do escoamento a
13-90 A vazão da água em um canal largo horizontal com 4 m de largura está sendo medida com um reservatório retangular de soleira espessa de 0,75 m de altura que abrange todo o canal. Se a profundidad
13-91 Repita o Problema 13-90 para o caso de um reservatório com 1 m de altura.
13-93 Considere um escoamento de água uniforme em um canal largo retangular com profundidade de 2 m e feito de concreto não polido com uma inclinação de 0,0022. Determine a vazão de escoamento da água