Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 103
Em uma festa surpresa para um amigo, você amarrou uma série de balões inflados com o gás hélio com diâmetro de 20 cm a um mastro de bandeira, Cada amarra com um pequeno cordão. O primeiro é amarrado a 1 m acima do solo, e os outros oito são amarrados a espaçamentos de 1 m, de modo que o último é amarrado a uma altura de 9 m. Sendo um engenheiro completamente nerd, você nota que para vento em regime permanente, cada balão é soprado pelo vento de forma que parece que os ângulos que os cordões fazem com a vertical são respectivamente em torno de 10°, 20°, 30°, 35°, 40°, 45°, 50°, 60° e 65°. Estime a trace um gráfico do perfil de velocidade do vento para a faixa de 9 m. Considere que o gás hélio está a 20°C e 10 kPa (manométrica), e que cada balão é feito com 3 gramas de látex.
Passo 1
Beleza! Então, para começar esse exercício, vamos escrever a equação para o coeficiente de arrasto:
E, sabemos também que a força no balão pode ser escrita como:
Então, vamos aplicar um equilíbrio de forças na direção , onde temos:
E, agora, na direção , onde teremos:
Beleza, então, vamos precisar das propriedades do ar e do hélio. Então, consultando as tabelas do apêndice A e considerando a pressão atmosférica como 101 kPa, teremos para o hélio:
E, a densidade do hélio será:
Agora, da mesma forma, para o ar, teremos:
E, a densidade do hélio será:
Passo 2
Agora, vamos retornar à equação de equilíbrio de forças na direção , onde temos:
Então, sabemos que a força resultando no balão será a diferença entre a densidade do ar e do hélio vezes a gravidade e o volume do balão, de modo que podemos escrever:
Então, substituindo os valores conhecidos na equação de cima, temos:
Agora, recorrendo a equação do passo 1 para o equilíbrio de forças na direção , temos:
E, substituindo a expressão encontrada para :
Passo 3
Então, o que precisamos fazer agora é analisar os diferentes balões e as forças a que eles estarão sujeitos, então, para o primeiro balão, temos , então a equação para a força de arrasto se torna:
Vamos usar o valor de da figura apresentada na Figura 9.11, pois é um intervalo de praticamente constante com Reynolds, só devemos checar se o valor de Reynolds obtido está dentro dessa faixa, então, teremos:
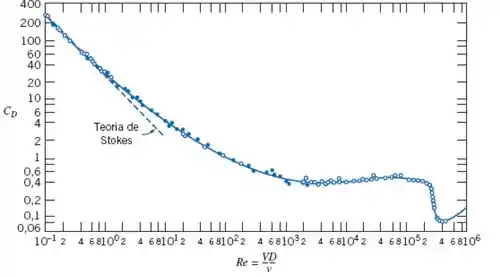
Então, para , da equação escrita no passo 1, temos:
Então, substituindo os valores conhecidos, temos:
Então, para essa velocidade devemos checar o número de Reynolds, para ver se usamos o coeficiente de arrasto correto, que é dado por:
Para isso, precisamos pegar o valor de no apêndice A, então temos:
Então, Reynolds será:
Esse valor está dentro da faixa.
Passo 4
Agora devemos fazer exatamente os mesmos cálculos, só que para os próximos balões, com diferentes ângulos , então, para não escrever novamente as mesmas equações, só mudando os valores, vamos resumir aqui os resultados, lembrando que o procedimento é o mesmo feito no passo 3. Então, teremos:
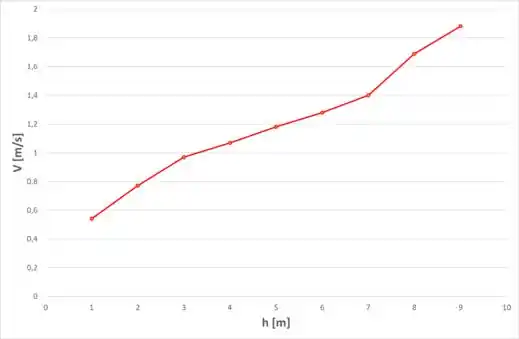
Então, com todos os valores de velocidade, podemos traçar o perfil de velocidade pedido no enunciado:
