Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 31
Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a distribuição de tensão de cisalhamento em uma camada limite laminar sobre uma placa plana. Trace versus . Compare com os resultados deduzidos a partir do perfil de velocidade aproximado senoidal dado no Problema 9.10.
Passo 1
Beleza! Então, para começar esse exercício, vamos escrever a equação para o perfil de velocidade senoidal:
E, sabemos que a tensão de cisalhamento pode ser escrita como:
E, de acordo com Blasius, temos o perfil de velocidade dado por:
Sendo que é dado por:
Sendo assim, a tensão de cisalhamento pode ser escrita como:
Então, a tensão de cisalhamento será:
Passo 2
Agora nós vamos pegar a equação encontrada no passo 1 para a tensão de cisalhamento e dividir os dois lados por , então, temos:
E, nós sabemos que o número de Reynolds é dado por:
Então a equação acima se torna:
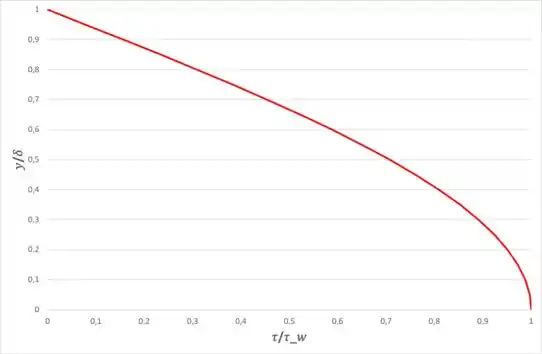
Então, a distribuição da tensão de cisalhamento, com o auxílio da tabela 9.1 apresentada nesse capítulo, pode ser representada por:
E, como temos , então:
Passo 3
Agora, do perfil senoidal, temos que a tensão de cisalhamento será:
Então, a derivada do perfil parabólico com relação à será:
Então, a tensão de cisalhamento se torna:
E, como temos:
Então, o perfil de cisalhamento será:
Plotando o perfil de cisalhamento, temos:
