Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 50
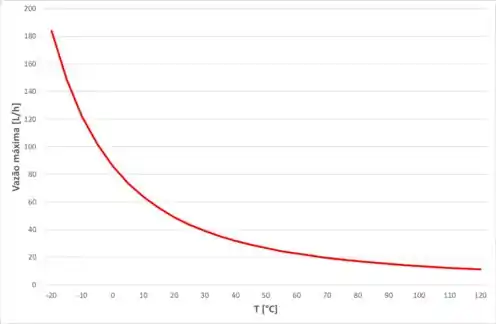
Usando a Eq. A.3 no Apêndice A para a viscosidade da água, encontre a viscosidade da água a -20 °C e 120 °C. Trace o gráfico da viscosidade para essa faixa de temperatura. Encontre a vazão laminar máxima (L/h) em um tubo de diâmetro 7,5 mm para essas temperaturas. Trace o gráfico da vazão laminar máxima para essa faixa de temperatura.
Passo 1
A primeira coisa que devemos fazer é ir no apêndice A e pegar a equação A.3, que é descrita a seguir:
E, agora, pegar também os valores das constantes e , que também estão no apêndice A, então, teremos:
Então, agora podemos calcular a viscosidade da água a -20 °C = 253,15 K e a 120 °C = 393,15 K, então, teremos:
Agora desenhando o gráfico da viscosidade para essa faixa de temperatura, temos:
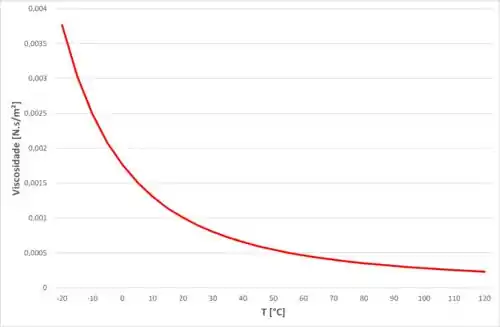
Passo 2
Agora, para encontrar a vazão laminar máxima, vamos considerar o estado para o Reynolds crítico, que é:
Então, a fórmula para o número de Reynolds crítico é dada por:
Agora podemos escrever a velocidade crítica em função da vazão máxima, então, teremos:
Então, substituindo essa expressão na equação acima, temos:
Passo 3
Então, para a temperatura , temos:
Convertendo para L/h, temos:
E, para a temperatura , temos:
Convertendo para L/h, temos:
E, a vazão máxima para essa faixa de temperatura será:
