Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 41
Na Figura 2.5 fica evidente que, em uma larga faixa de temperatura, a dependência com a temperatura da condutividade térmica de muitos sólidos pode ser aproximada por uma expressão linear que tem a forma , na qual ke é uma constante positiva e a é um coeficiente que pode ser positivo ou negativo. Obtenha uma expressão para o fluxo térmico através de uma parede plana cujas superfícies interna e externa sejam mantidas a T0 e T1, respectivamente. Esboce as formas da distribuição de temperaturas que correspondem a a > 0, a = 0 e a
Passo 1
Beleza galerinha, vamos lá! Para as condições assumidas, qx e A(x) são constantes e Eq. 3.26 dá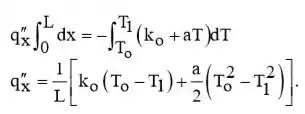
Da lei de Fourier:
Passo 2
Assim, como o produto de (ko+aT) e dT/dx) é constante, diminuindo T com aumento de x implica,
a > 0: decrescente (ko+aT) e crescente |dT/dx| com aumento x
a = 0: k = ko => constante (dT/dx)
a
Resposta
a > 0: decrescente (ko+aT) e crescente |dT/dx| com aumento x
a = 0: k = ko => constante (dT/dx)
a