Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 36
Na figura abaixo o tanque e o tubo estão abertos a atmosfera. Se L = 2,13 m, qual é o ângulo de inclinação do tubo?
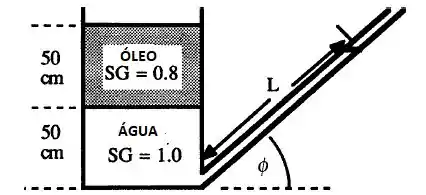
Passo 1
Como os recipientes estão abertos pra atmosfera, a primeira coisa que precisamos entender é que vamos usar a hidrostática e que essas pressões devem ser iguais a pressão atmosférica.
IMPORTANTE: O sinal de subtração na contribuição do tubo inclinado é porque devemos lembrar sempre que em problemas desse tipo, “somamos” as colunas de água que tem sentido “de cima pra baixo” e subtraímos as colunas que tem sentido “de baixo pra cima” de acordo com a orientação que estamos montando nossa equação de hidrostática.
Por exemplo, estamos indo do topo do tanque até o tubo aberto inclinado, então as colunas de óleo e água do tanque tem orientação de cima pra baixo (somar) enquanto a coluna de água do tubo inclinado cresce de baixo pra cima (subtração).
Passo 2
Bem, mas como calculamos a pressão que essa coluna de água de forma inclinada está exercendo sobre meu processo?
Bem, meu camarada, para isso você precisa lembrar que não importa a angulação que esteja meu tubo, para calcular a pressão em um determinado ponto, eu só preciso conhecer qual é a altura vertical da coluna de fluido em cima deste ponto.
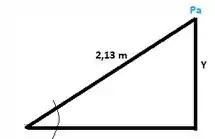
Portanto, a altura vertical será dada por
Passo 3
Escrevendo então novamente nossa equação de hidrostática:
Dada as densidades SG, podemos calcular as densidades absolutas dos fluidos, já que .
Dado que e podemos encontrar o valor do ângulo como sendo:
OBS: Considere gravidade igual a 10 m/s².