Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 61

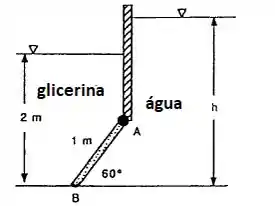
A comporta AB na figura abaixo é uma massa homogênea de 180 kg, 1,2 m de largura, é articulada em A e está apoiada sobre um fundo liso em B. Todos os fluidos estão a 20°C. Para qual profundidade h da água a força no ponto B será zero?

Passo 1

Primeira coisa é pegar nossas velhas e boas amigas densidades de cada fluido!!

ρ á g u a = 979   k g / m ³

ρ g l i c e r i n a = 1236   k g / m ³

Primeira coisa que precisamos também determinar é sua altura de centroide, ou seja, a altura “vertical” da placa inclinada. Para isso basta usarmos trigonometria tal que y seja a distância entre o ponto A e o chão.

s e n 60 ° = y 1 → y = 0,866 → h C G = y 2 = 0,433   m

O centroide da placa estará a 0,433 m verticalmente abaixo do ponto A. Isso vai dizer pra gente que a nossa altura de centroide é dada em h C G = 2 - 0,433 = 1,567   m e agora com esse valor, podemos calcular qual é a força hidrostática que a glicerina estará fazendo na nossa placa, beleza?

F g = ρ g l i c e r i n a g h C G A = 1236 x 10 x 1,567 x 1,2 x 1 = 23242   N

Vamos aproveitar e calcular a altura de centro de pressão:

y C P , g = - I X X s e n θ h C G A = - b L 3 12 s e n θ h C G A = - 1,2 x 1 3 12 s e n 60 ° 1,567 x 1 x 1,2 = - 0,0461   m

Passo 2

De posse agora do valor de y C P , g vamos desenhar um diagrama de corpo livre pra entendermos os balanços de força, show?

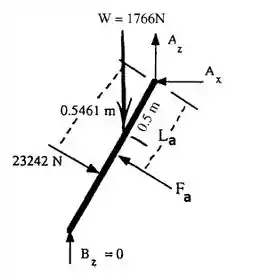
A força de água e sua linha de ação estão mostradas sem números porque elas dependem da profundidade que está o centroide da comporta do lado da água. Note que a distância de atuação da força que a glicerina faz é igual a metade da placa somado ao valor de distância de centro de pressão, ok?

F a = ρ á g u a g h C G A = 979 x 10 x h C G x 1,2 x 1 = 9790 h C G 1,2

y C P , a = - I X X s e n θ h C G A = - b L 3 12 s e n θ h C G A = - 1,2 x 1 3 12 s e n 60 ° h C G x 1 x 1,2 = - 0,0 722 h C G

Passo 3

Sabemos que o peso do portão é dado por W = 180 x 9,81 = 1766 N, e que esse carinha vai atuar no centroide como mostrado na figura no passo 2. Considerando que a força Bz seja igual a zero, podemos somar os momentos que atuam em A de forma a encontrar a profundidade de água. Se liga!!!

∑ M A = F g h g + F p e s o d - F a L a = 0

∑ M A = 23242 x 0,5461 + 1766 0,5 c o s 60 ° - 9790 h C G 1,2 0,5 + 0,0722 h C G = 0

Resolvendo para hCG, temos:

h C G = 2,09   m → h = h C G + 0,433 = 2,52   m

Resposta

h = 2,52   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta AB na figura abaixo tem 1,5 m de largura, está articulada em A e limitada por um limitador em B. A água está a 20°C. Calcule (a) a força no limitador B e (b) as reações em A se a profundida
O exemplo 2.5 calculou a força na placa AB e sua linha de ação, usando a abordagem de momento de inércia. Alguns professores dizem que é mais instrutivo calcular esses valores por integração direta da
Repita o problema P2.77 para deduzir uma expressão analítica para P em função e h. Há alguma coisa incomum na sua solução?
Na figura abaixo, a comporta AB fecha uma abertura circular de 80 cm de diâmetro. A comporta é mantida fechada por uma massa de 200 kg como mostrado. Suponha a gravidade padrão a 20°C. Em que nível h
A comporta circular ABC na figura abaixo tem um raio de 1 m e é articulada em B. Calcule a força P exatamente suficiente para impedir que a comporta se abra quando h = 8 m. Despreze a pressão atmosfér