Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 69
Considere a placa inclinada AB com comprimento L na figura abaixo. (a) A força hidrostática sobre a placa é igual ao peso da água que está faltando acima da placa? Se não for, corrija essa hipótese. Despreze a atmosfera. (b) Pode a teoria da “água que falta” ser generalizada para superfícies curvas desse tipo?
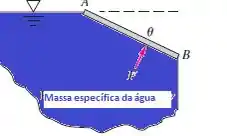
Passo 1
Vamos descobrir qual é a altura do ponto B em relação a atmosfera, beleza?
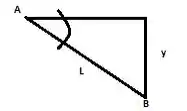
Show, a gente sabe que para uma placa plana, o centroide dela estará em e vamos assumir que a placa tem largura b para podermos calcular a área dela e por consequência a força hidrostática:
Passo 2
(a) Assumindo que a placa tem massa m, sabemos que a força peso atuará no centro da placa, ou seja, também atuará em L/2.
Olhando para o diagrama de corpo livre, temos:
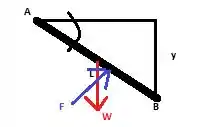
Vamos agora calcular onde a linha de atuação da força F estará atuando:
Passo 3
Somando-se os momentos no ponto A por exemplo, temos:
Aqui notamos que a força hidrostática sobre a placa NÃO é igual ao peso da água que está faltando acima da placa e que sua correção está atrelada ao fator
Passo 4
(b) Essa generalização pode ser apenas feita quando temos a física semelhante a esta, ou seja, apenas força hidrostática e peso atuando sobre uma placa plana.
Resposta
Ei, a resposta está no passo a passo :)