Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 29

A figura mostra o escoamento através de uma comporta. Estime a profundidade da água e a velocidade depois da comporta (bem antes do ressalto hidráulico).

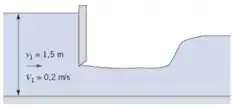
Passo 1

Precisamos estimar a profundidade e há velocidade depois da comporta...Vamos lá!

Partindo da da equação da Energia:

E 1 = V 1 2 2 g + y 1

Como o enunciado nos deu:

y 1 = 1,5   m V 1 = 0,2   m / s

Podemos encontrar o E 1 :

E 1 = 0,2 2 2 * 9,8 + 1,5

E 1 = 1,50   m

Passo 2

Beleza! Se a gente já encontrou o E 1 e sabemos que bem depois do ressalto, E 1 = E 2 , podemos concluir o seguinte:

E 1 = V 2 2 2 g + y 2

em, não temos o V 2 , mas podemos usar há relação de velocidade com a vazão, já que há vazão será a mesma:

Q = V * A

Q = V * y

Q = V 1 * y 1 Q = V 2 * y 2

V 2 = Q y 2

Agora nós podemos substituir o V 2 :

E 1 = Q y 2 2 2 g + y 2

Passo 3

Nessa equação que descobrimos no passo 2, só falta a gente achar o y 2 , por que a vazão podemos tirar assim:

Q = V 1 * y 1

Q = 0,2 * 1,5

Q = 0,3   m 2 s

Beleza! Agora há gente pode atribuir valores para y 2 até que a resposta dessa equação seja o nosso E 1 :

y 2 = 0,5 0,3 y 2 2 2 * 9,8 + y 2 = 0,518   m

y 2 = 0,05 0,3 y 2 2 2 * 9,8 + y 2 = 1,89   m

y 2 = 0,0563 0,3 y 2 2 2 * 9,8 + y 2 = 1,50   m

Passo 4

Aeeee! Já achamos o valor da profundidade, agora partiu achar a velocidade:

V 2 = Q y 2

V 2 = 0,3 0,0563

V 2 = 5,33   m / s

Uhul!! Acabamos!!

Resposta

y 2 = 0,0563   m V 2 = 5,33   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um canal retangular para água pluvial, em concreto bruto, deve carregar uma vazão máxima de 2,83m 3 / s , em condição crítica. Determine a largura e a inclinação do canal.
Um canal trapezoidal forrado com tijolo tem lados inclinados de 2 : 1 e largura de fundo de 3m . Ele carrega 17m 3 / s a velocidade crítica. Determine a inclinação crítica (a inclinação na qual a prof
Um conduto retangular construído de concreto, com inclinação de 1 m por 1000 m, tem 1,8 m de largura. Água escoa a uma profundidade normal de 0,9 m. Calcule a descarga.
Água escoa em um canal trapezoidal a uma profundidade normal de 1,2 m. A largura do fundo é de 2,4 m e a inclinação lateral é de 1:1 ( 45 ° ). A vazão é 7,1 m 3 s . O canal é escavado na terra nua. De
Um canal retangular com 2 m de largura e inclinação de 0,0005 possui uma profundidade de escoamento de 1,5 m. O coeficiente de rugosidade de Manning é de 0,015. Determine a descarga uniforme em regime