Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 95
Para as condições descritas no Problema 1.44, determine a distribuição de temperaturas, , no recipiente, expressando o seu resultado em termos de e da condutividade térmica dos rejeitos radioativos.
Passo 1
Beleza! Então, como temos um cilindro e temos geração no problema, vamos utilizar a equação do calor para sistemas radiais com geração, então, temos:
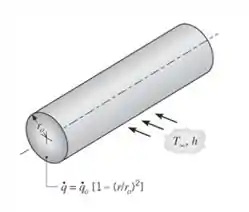
Agora vamos substituir a expressão para dada na figura do Problema 1.44, então, a equação do calor se torna:
Passo 2
Agora, integrando a equação obtida no passo 1 em , temos:
E, integrando novamente essa expressão, chegamos em:
Passo 3
Agora, para encontrar as constantes e , vamos aplicar as condições de contorno conhecidas, que são a de temperatura constante no centro do cilindro, ou seja:
Então, substituindo esses valores na equação obtida no passo 2, temos:
Então, para que não tenhamos nenhuma indeterminação, devemos ter:
Agora, a segunda condição é a de que na superfície, teremos a troca de calor por condução se igualando à por convecção, então, temos:
Então, substituindo as expressões conhecidas, temos:
Dessa forma, o perfil de temperatura será: