Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 99
Seja a configuração do Exemplo 3.8, na qual o aquecimento volumétrico uniforme em um tubo de aço inoxidável é induzido por uma corrente elétrica e o calor é transferido por convecção para o ar que escoa no seu interior. A parede do tubo possui raios interno e externo de = 25 mm e = 35 mm, uma condutividade térmica k = 15 W/(m · K), uma resistividade elétrica , e uma temperatura de operação máxima permissível de 1400 K.
(a) Supondo a superfície externa do tubo perfeitamente isolada e o escoamento do ar caracterizado por uma temperatura e coeficiente convectivo = 400 K e = 100 W/(m² · K), determine a corrente elétrica máxima permissível I.
(b) Calcule e represente a distribuição de temperaturas radial na parede do tubo para a corrente elétrica da parte (a) e três valores de (100, 500 e 1000 W/(m² · K)). Para cada valor de , determine a taxa de transferência de calor para o ar, por unidade de comprimento do tubo.
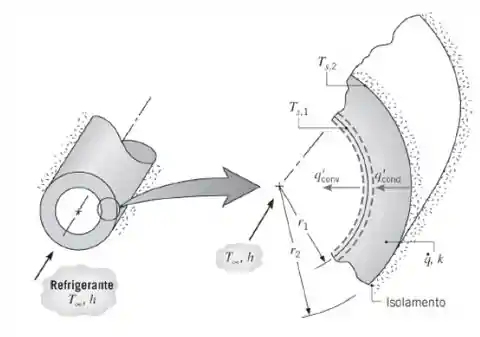
(c) Na prática, mesmo o melhor dos materiais isolantes seria incapaz de manter condições adiabáticas na superfície externa do tubo. Considere o uso de um material isolante refratário com condutividade térmica k = 1,0 W/(m · K) e despreze a troca radiante na sua superfície externa. Para = 100 W/(m² · K) e a corrente máxima permissível determinada na parte (a), calcule e represente a distribuição de temperaturas na parede composta para dois valores da espessura da camada de isolante (δ = 25 e 50 mm). A superfície externa do isolante está exposta ao ar ambiente, para o qual = 300 K e = 25 W/(m² · K). Para cada espessura do isolante, determine as taxas de transferência de calor, por unidade de comprimento do tubo, para a corrente de ar no interior do tubo e para o ambiente.
Passo 1
Beleza! Vamos começar esse exercício aproveitando o desenvolvimento feito no Exemplo 3.8 dessa seção do livro, onde se chegou na seguinte equação para o perfil de temperatura:
Então, substituindo , para descobrir a temperatura na superfície interna, nessa equação, temos:
Agora, ainda do Exemplo 3.8, utilizando a equação 10 obtida, temos:
Agora, igualando as duas expressões encontradas para , chegamos em:
Substituindo os valores conhecidos, chegamos em:
Então, como a temperatura de operação máxima permissível é de 1400 K, e essa temperatura ocorrerá em , e nós temos que , então, substituindo esses valores na expressão de cima, obtemos um valor para :
Passo 2
Agora, sabendo que a taxa de geração de calor será dada pela potência pelo volume, temos:
No entanto, a potência pode ser escrita em função da resistência e da corrente da seguinte forma:
E, por sua vez, escrevendo a resistência em função da resistividade elétricada dada no enunciado, temos:
Em que é o comprimento do bastão e é a sua seção transversal. Agora, da mesma forma, o volume do bastão pode ser escrito como:
Então, substituindo as expressões para e na equação para , obtemos:
Substituindo os valores conhecidos, chegamos em:
Passo 3
Agora, para a letra (b), nós vamos analisar a equação utilizada no passo 1 para o perfil de temperatura:
E de temos:
Então, como podemos ver da equação para , a diferença entre as temperaturas nos pontos 1 e 2 não muda com o valor de , o que muda será a temperatura 1. Então, calculando nos três casos, temos:
Como a corrente é a mesma utilizada na letra (a), então a geração de calor será a mesma. Dessa forma, a taxa de transferência de calor para o ar, em será: