Considere os fardos cilíndricos de feno no Problema 3.82. É proposto usar a geração microbiológica de energia associada ao feno molhado para aquecer água. Considere um tubo com de diâmetro, com parede delgada, inserido na direção longitudinal no centro de um fado cilíndrico. O tubo transporta água a , com .
(a) Determine a taxa de transferência de calor, em regime estacionário, para a água, por unidade de comprimento do tubo.
(b) Represente graficamente a distribuição radial de temperaturas no feno, .
(c) Represente graficamente a transferência de calor para a água, por unidade de comprimento do tubo, para diâmetros do fardo na faixa .
Passo 1
Fala galera!!
Nessa questão, queremos obter: (a) Transferência de calor em estado estacionário para a água por unidade de comprimento do tubo, (b) Gráfico da distribuição da temperatura radial, T (r), no feno (c) Gráfico da transferência de calor para a água por unidade comprimento do tubo para diâmetros de fardo de para .
Para isso, podemos fazer o diagrama esquemático de um fardo cilíndrico de feno com o tubo passando dentro.
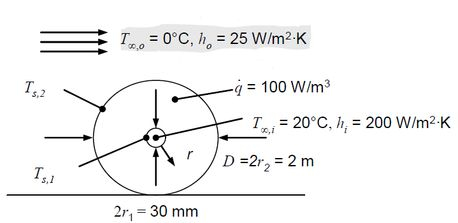
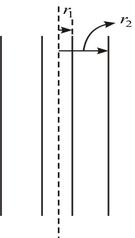
Também podemos fazer o diagrama do tubo de raio de parede fina, inserido longitudinalmente no meio de um fardo cilíndrico de feno.
Passo 2
PRESSUPOSTOS:
(1) Condições em estado estacionário;
(2) Propriedades constantes;
(3) Transferência de calor unidimensional;
(4) Geração volumétrica uniforme;
(5) Radiação desprezível;
(6) Condução desprezível de ou para o solo.
DADOS FORNECIDOS:
Diâmetro do fardo cilíndrico de feno:
Raio do fardo cilíndrico de feno:
Diâmetro do tubo:
Raio do tubo:
Condutividade térmica do feno no fardo:
Taxa volumétrica de geração de calor uniforme para o feno molhado:
Temperatura ambiente:
Coeficiente de transferência de calor por convecção:
Temperatura da água que passa no tubo:
Coeficiente de transferência de calor do tubo para a água:
Passo 3
Para resolver esse problema, vamos precisar da distribuição de temperatura para um cilindro em que ocorre a geração interna de calor. Podemos obter utilizando a solução geral dada pela Eq. 3.56 com condições de contorno mistas aplicadas em e . Especificamente,
Para :
Para
Temos que a Eq. 3.56 é a seguinte:
Aqui, é o calor interno gerado, é a condutividade térmica do material, é o raio do cilindro e e são as constantes de integração.
Passo 4
Agora vamos procurar e aplicando as condições de contorno. Pela primeira condição temos o seguinte:
Substituindo os temos da expressão acima, temos:
Passo 5
Pela segunda condição temos o seguinte:
Substituindo os temos da expressão acima, temos:
Passo 6
Subtraindo a equação encontrada no passo 4 com a equação encontrada no passo 5, temos o seguinte:
Substituindo os temos da equação acima pelos dados fornecidos, temos que é o seguinte:
Passo 7
Da equação encontrada no passo 5 temos o seguinte:
Substituindo os termos da equação pelos dados obtidos, temos o seguinte:
Passo 8
Temos então que:
Substituindo na solução geral da distribuição de temperatura temos que a equação fica da seguinte maneira:
Substituindo e , temos que a equação fica da seguinte forma:
Passo 9
(a) Com a equação da distribuição de temperatura, vamos calcular a temperatura na superfície interna do tubo de parede fina. Assim, para temos o seguinte:
Agora, vamos calcular a taxa de transferência de calor em estado estacionário usando a equação de convecção. Assim temos:
Aqui, é o coeficiente de convectivo ente a água e o tubo, é a área da superfície interna, é a temperatura da superfície do tubo, é temperatura da água, é o raio do tubo e é a taxa de transferência de calor por comprimento do tubo. Substituindo os termos da equação pelos dados fornecidos temos:
Portanto, a taxa de transferência de calor em estado estacionário é .
Passo 10
(b) Agora, vamos representar graficamente a distribuição radial de temperaturas no feno, . Para isso, vamos calcular o raio do feno úmido na temperatura máxima.
A temperatura quando é é a seguinte:
Usando a distribuição de temperatura que encontramos podemos fazer a seguinte tabela:
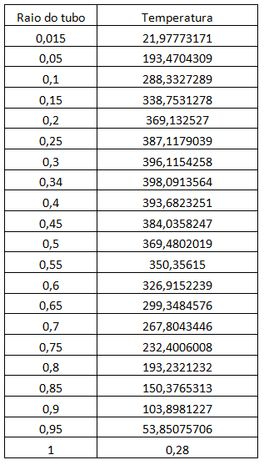
Com a tabela podemos traçar a distribuição radial da temperatura no feno. Assim temos:
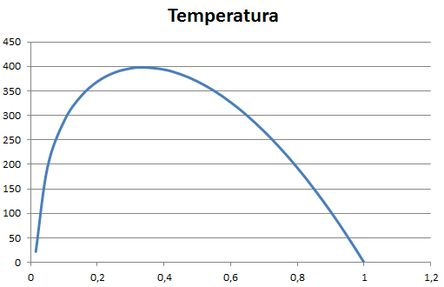
Passo 11
(c) Para resolver essa questão, vamos precisar de da equação que encontramos para
da equação que encontramos para
da solução geral da distribuição de temperatura que encontramos
e também da equação para a taxa de transferência de calor
Com essas 4 equações, nós podemos fazer a seguinte tabela em função do raio feno .
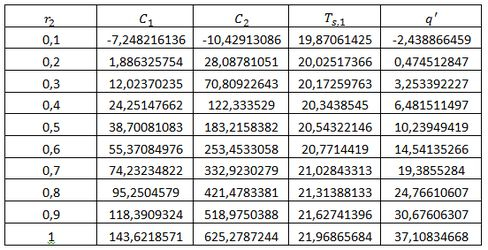
Agora, podemos plotar o gráfico da transferência de calor por unidade de comprimento do tubo para a água em função do diâmetro do feno. Neste caso representamos pelo raio.
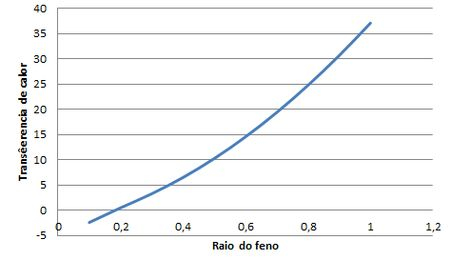
Resposta
(a)