Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 13

Na figura a seguir, o sistema está em equilíbrio estático. Pede-se:

  1. p a r 1 em m m H g a b s ;
  2. p a r 2 em m c a .

Dados: D = 71,4   m m ; d = 35,7   m m ; h = 400   m m ; p a t m = 684   m m H g ; γ H g = 136000   N / m 3 ; para F = 0 ⇒ h = 0 .

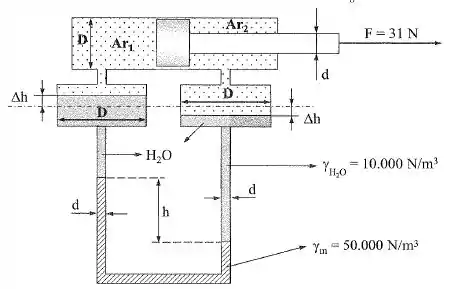
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A pressão absoluta do ar na região 1 é dada por:

p a r 1 π D 2 4 + F = p a r 2 π 4 D 2 - d 2

p a r 1 π 0,0714 2 4 + 31 = p a r 2 π 4 0,0714 2 - - 0,0357 2

4 ⋅ 10 - 3 p a r 1 + 31 = 3 ⋅ 10 - 3 p a r 2

Passo 2

Aplicando a equação manométrica no sistema, teremos:

p a r 1 + 2 γ H 2 O ∆ h + γ m h - γ H 2 O h = p a r 2

Temos também que:

∆ h π D 2 4 = h 2 π d 2 4

Logo:

∆ h = h 2 d D 2

∆ h = 0,4 2 35,7 71,4 2

∆ h = 0,05   m  

Logo, teremos que:

p a r 1 + 2 10000 0,05 + ( 50000 ) ( 0,4 ) - ( 10000 ) ( 0,4 ) = p a r 2

p a r 1 + 17000 = p a r 2

Passo 3

Agora podemos substituir e relacionar as equações encontradas:

4 ⋅ 10 - 3 p a r 1 + 31 = 3 ⋅ 10 - 3 p a r 1 + 17000

p a r 1 = 20000

Logo:

p a r 1 = 20000 136000 = 0,147   m

Ou:

p a r 1 = 147   m m H g

Sendo assim a pressão absoluta igual a:

p a r 1 a b s = 137 + 684

p a r 1 a b s = 831   m m H g   ( a b s )

Passo 4

A pressão na região 2 é dada por:

p a r 2 = p a r 1 + 17000

p a r 2 = 37000

Ou:

p a r 2 = 37000 10000

p a r 2 = 3,7   m c a

Resposta

a )   p a r 1 a b s = 831   m m H g   ( a b s )

b )   p a r 2 = 3,7   m c a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cubo com arestas de 150mm, suspenso por um fio, está submerso em um líquido de modo que sua face horizontal superior está 203 mm abaixo da superfície livre. A massa do cubo é M = 29 kg e a temperat
Um manômetro de reservatório tem tubos verticais com diâmetros D=18m m e d=6m m . O líquido manométrico é o óleo Meriam vermelho. Desenvolva uma expressão algébrica para a deflexão do líquido, L, no t
Veículos de pesquisa oceanográfica já desceram a 10 km abaixo do nível do mar. Nessas profundidades extremas, a compressibilidade da água do mar pode ser significativa. O comportamento da água do mar
O manômetro mostrado contém água e querosene. Com ambos os tubos abertos para a atmosfera, as elevações da superfície livre diferem de H 0 = 20,0 mm. Determine a diferença de elevação quando uma press
Para que o módulo de compactação seja constante para a água do mar, deduza uma expressão para variação da massa específica com profundidade, h, abaixo da superfície. Mostrar que o resultado pode ser e