Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 11

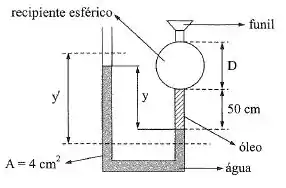
No sistema da figura, na situação inicial a esfera está vazia. Introduz-se óleo pelo funil até preencher totalmente o recipiente esférico e y passa a valer y ' = 1   m . Dados: γ ó l e o = 8000   N / m 3 ; γ H 2 O = 10000   N / m 3 .

  1. Qual é o valor de y na situação inicial?
  2. Qual é o diâmetro da esfera?
  3. Qual é o volume de óleo introduzido para estabelecer a situação final?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão fazendo um esqueminha pra marcaros os pontos!

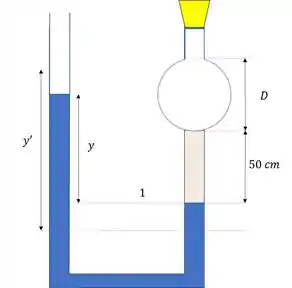
A primeira coisa que a gente quer é achar y na situação inicial, ou seja, quando a esfera ainda esta vazia!

Na linha 1 temos dois pontos onde as pressões são iguais, pois estão na mesma altura e o fluido é o mesmo! Então podemos escrever:

γ ó l e o ⋅ 50 = γ H 2 O ⋅ y

y = 8000 ⋅ 50 10000

y = 40   c m

Ou

y = 0,4   m

Passo 2

Agora a gente quer saber o diâmetro da esfera! Então vamos lá!

O problema disse pra a gente que quando a esfera esta cheia, o valor de y passa a valer y ' = 1 m .

Além disso a coluna de água se desloca, e a situação que a gente passa a ter é essa daqui:

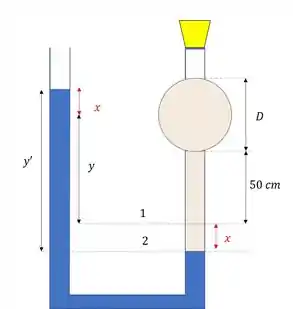
Considerando que na linha dois a gente tem dois pontos com pressões iguais:

γ ó l e o ⋅ D + 0,5 + x = γ H 2 O ⋅ y '

A gente só precisa achar o x para descobrir o D !

Podemos dizer que:

y + 2 x = y '

Como y ' = 1   m e y = 0,4   m , teremos que:

x = 1 - 0,4 2

x = 0,3   m

Logo:

8000 ⋅ D + 0,5 + 0,3 = 10000 ⋅ 1

D = 10000 8000 - 0,8

D = 0,45   m

Passo 3

Por fim a gente quer saber o volume de óleo que foi introduzido!!

O volume do óleo sera a soma do volume da esfera com o volume do cilindro, certo?

V = π D 3 6 + x A

O problema nos da A = 4   c m 2 , como o diâmetro esta em metro, vamos passar a área para metro também:

A = 4   c m 2 × 1   m 2 10 2   c m 2 = 4 × 10 - 4 m 2  

V = π 0,45 3 6 + 0,3 4 × 10 - 4

V = 4,78 × 10 - 2   m 3

Resposta

y = 0,4   m

D = 0,45   m

V = 4,78 × 10 - 2   m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água flui para baixo ao longo de um tubo inclinado de 30º em relação à horizontal conforme mostrado. A diferença de pressão p A - p B é causada parcialmente pela gravidade e parcialmente pelo atrito.
O manômetro mostrado contém dois líquidos. O líquido A tem densidade relativa 0,88 e o líquido B 2,95. Calcule a deflexão, h, quando a diferença de pressão aplicada é p 1 – p 2 = 860P a .
Um reservatório com dois tubos cilíndricos verticais de diâmetros d 1 =39,5m m e d 2=12,7m m é parcialmente preenchido com mercúrio. O nível de equilíbrio do líquido é mostrado no diagrama da esquerda
Um recipiente cilíndrico é imerso vagarosamente de “boca para baixo” em uma piscina. O ar aprisionado no recipiente é comprimido isotermicamente enquanto a pressão hidrostática aumenta. Desenvolva uma
Compare uma altura devido à ação capilar da água exposta ao ar em um tubo circular de diâmetro D = 0,5 mm, e entre duas placas planas verticais infinitas com espaçamento a = 0,5 mm entre elas.