Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 110
A figura a seguir, tem a entrada do tubo como um canto vivo. Se a vazão é de 0,004 m³/s, qual a potência, em W, extraída pela turbina?
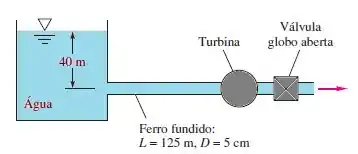
Passo 1
Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!
Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.
Bem, os tubos são feitos de ferro fundido, ou seja, todos eles devem possuir a mesma rugosidade , portanto a rugosidade relativa é:
Passo 2
A vazão é conhecida, então cada velocidade, número de Reynold e f podem ser calculados, show de bola?
Bem, sabemos como se calcula Reynold e a relação de velocidade com a vazão, então podemos escrever que:
Olha no gráfico de Moody, vamos observar que para esse valor de Reynold e com a rugosidade relativa de 0,005 temos um valor de (É importante ressaltar que você não precisa necessariamente encontrar o mesmíssimo valor ou idêntico ao meu valor de f, mas a ordem de grandeza deve estar próxima).
Passo 3
Agora vamos procurar na tabela do livro quais são os coeficientes dos “acidentes” que temos durante o caminho que o fluido percorre, beleza?
E quais são esses acidentes:
- Entrada no tanque,
- Válvula globo aberta,
Passo 4
A equação de Bernoulli será a principal para resolver esse problema e determinarmos a potência que o exercício pede, beleza?
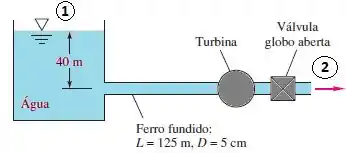
Temos que no ponto 1 e 2 as pressões são iguais a pressão atmosférica. Outra hipótese é que na superfície do tanque a velocidade será aproximadamente zero. Com essas hipóteses, nossa equação se reduzirá em:
Lembrando que o nosso hf e hm estão associados às perdas de carga maiores e menores, respectivamente.
Onde
Substituindo os valores respectivos, ao final obtemos que
Passo 5
A potência resultante para turbina pode ser calculada como sendo: