Filas de módulos termoelétricos do Exemplo 3.13 estão fixadas na placa plana absorvedora do Problema 3.108. As filas de módulos estão separadas por e a parte inferior dos módulos é resfriada por água a uma temperatura de , com .

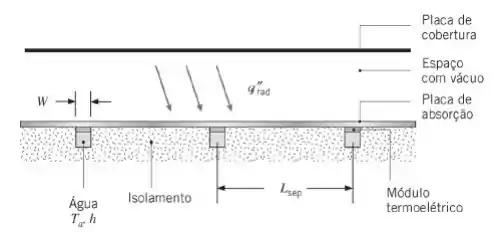
Determine a potência elétrica produzida por uma fila de módulos termoelétricos conectados eletricamente em série com uma resistência carga de . Calcule a taxa de transferência de calor para a água escoando nos canais. Suponha filas com módulos colocados um junto ao outro, com comprimento da fila e do tubo de água iguais a , com , a dimensão do módulo retirada do Exemplo 3.13. Despreze resistências térmicas de contato e a queda de temperatura ao longo da parede do tubo, e suponha que a alta condutividade térmica da parede do tubo crie uma temperatura uniforme ao redor do seu perímetro. Em função da resistência térmica presente devido aos módulos termoelétricos, não é apropriado supor que a temperatura da placa de absorção, diretamente acima de um tubo, seja igual à temperatura da água.

Agora vamos encontrar quem é o nosso :

Se a nossa energia produzida é igual a nossa energia dissipada, vamos ter que:

E ainda está faltando o nosso , não podemos esquecer dele! Podemos encontrar ele por essa equação aqui olha só:

Agora podemos montar o que achamos em um sistema, olha só:

Sistema a gente já está acostumado a resolver, né?

Resolvendo esse carinha aí vamos ter que:

Agora é só retornar lá na nossa equação da potência:

E nossa transferência de calor total será:

Uhull! Conseguimos!