Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 22

Considere uma parede plana composta constituída por dois materiais com condutividades térmicas k A = 0,09   W / ( m · K ) e k B = 0,03   W / ( m · K ) e espessuras L A = 8   m m e L B = 16   m m . A resistência de contato na interface entre os dois materiais é conhecida, sendo 0,30   m 2 · K / W . O material A está em contato com um fluido a 200 ° C com h 1 = 10   W / ( m 2 · K ) , e o material B está em contato com um fluido a 4 0 ° C , no qual h 2 = 2 0   W / ( m 2 · K ) .

(a) Qual é a taxa de transferência de calor através de uma parede que tem 2   m de altura e 2,5   m de largura?

(b) Esboce a distribuição de temperaturas.

Passo 1

E aí, bom ter você aqui!

Vem comigo resolver essa questão!

Letra a)

Para calcularmos a taxa de transferência de calor utilizaremos a seguinte forma:

q = T ∞ , 1 - T ∞ , 2 R t o t

Mas, primeiro, devemos calcular a resistência total:

R t o t = 1 h 1 A + L A k A A + R t , c + L B k B A + 1 h 2 A

Substituindo os dados:

R t o t = 1 10 ⋅ 5 + 0,008 0,09 ⋅ 5 + 0,3 5 + 0,016 0,03 ⋅ 5 + 1 20 ⋅ 5

R t o t = 0,21   K / W

Substituído na equação de taxa de transferência de calor:

q = 200 - 40 0,21

q = 762   W

Passo 2

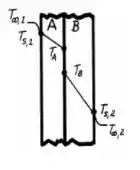
Letra b)

Agora, devemos esboçar a distribuição de temperaturas.

T s , 1 :

q = h 1 A T ∞ , 1 - T s , 1

762 = 10 ⋅ 5 ⋅ ( 200 - T s , 1 )

T s , 1 = 184,8 ° C

T A :

q = k A A L A T s , 1 - T A

762 = 0,09 ⋅ 5 0,008 ⋅ ( 184,8 - T A )

T A = 171,2 ° C

T B :

q = 1 R t , c T A - T B

762 = 1 0,06 ⋅ ( 1 71,2 - T B )

T B = 125,5 ° C

T s , 2 :

q = k B A L B ⋅ ( T B - T s , 2 )

762 = 0,03 ⋅ 5 0,016 ⋅ ( 125,5 - T s , 2 )

24684 = 25,4 0,024 ⋅ ( 137 - T s , 2 )

T s , 2 = 44,2 ° C

T ∞ , 2 :

q ' ' = h 2 A ( T s , 2 - T ∞ , 2 )

762 = 20 ⋅ 5 ⋅ 44 , 2 - T ∞ , 2

T ∞ , 2 = 36,6 ° C

Passo 3

Por fim, esboçando a distribuição de temperaturas

Até a próxima questão!

Resposta

q = 762   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

174 – Uma parede de 4m e 6m de comprimento é construída por duas grandes placas grossas de aço k = 15 W m ⋅ K de 2c m de espessura, separadas por barras de aço de 1c m de espessura e 22c m de largura
170 – Uma placa de circuito de 0,2c m de espessura, 10c m de altura e 15c m de comprimento contém, em um lado, componentes eletrônicos que dissipam uniformemente a taxa total de calor de 15W . A placa
185 – A parede de um armazém frigorifico tem 10,0m de altura e 5,0m de largura. A parede é feita de três camadas: alumínio k = 200 W m ⋅ K de 1,0c m de espessura, fibra de vidro k = 0,038 W m ⋅ K de 3
187 – Uma barra de 12 cm de comprimento com seção transversa quadrada, como a mostrada na Fig. P3-187, é constituída por uma camada de cobre k = 38 0 W m ⋅ K de 1c m de espessura e uma camada de epóxi
175 – Ar condicionado frio a 12℃ ℃ está fluindo dentro de um duto quadrado de alumínio k = 237 W m ⋅ K de 1,5c m de espessura e seção transversal interna de 22c m × 22c m , com vazão mássica de 0,8k g