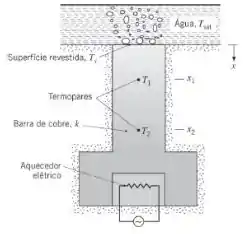
Um aparelho para efetuar experimentos de ebulição tem uma barra de cobre que tem uma de suas extremidades exposta a um líquido em ebulição e um aquecedor elétrico encapsulado na extremidade oposta, e encontra-se isolada termicamente da vizinhança em todas as suas superfícies, exceto a exposta ao líquido. São inseridos termopares na barra que são usados para medir as temperaturas em posições distantes e da superfície.

(a) Um experimento é efetuado para determinar as características de ebulição de um revestimento especial que é aplicado sobre a superfície exposta. Sob condições de regime estacionário, ebulição nucleada é mantida em água saturada à pressão atmosférica e valores e são registrados. Se , qual o valor do coeficiente associado à correlação de Rohsenow?

(b) Supondo a aplicabilidade da correlação de Rohsenow com o valor de determinado na parte (a), calcule e represente graficamente o excesso de temperatura como uma função do fluxo térmico na ebulição para . Quais são os valores correspondentes de e , para ? Se for aumentado para , podem os resultados anteriores ser extrapolados para inferir os valores correspondentes de ?

Para resolver essa questão vamos assumir: condução unidimensional em estado estacionário na barra, a água é saturada a e a aplicabilidade da correlação de Rohsenow com .

O coeficiente pode ser determinado se e forem conhecidos. Então, aplicando a lei de Fourier entre e temos,

Como a distribuição de temperatura na barra é linear,

Então,

Tendo que construímos,