Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 62

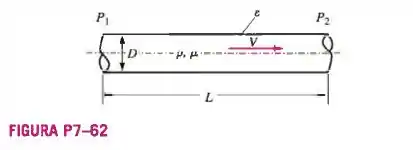
Um fluido incompressível de densidade ρ e viscosidade μ escoa a uma velocidade média V através de uma seção longa horizontal de tubo redondo de comprimento L , diâmetro interno

D e altura de rugosidade da parede interna ε (Figura P7-62). O tubo é suficientemente longo para que o escoamento seja completamente desenvolvido, significando que o perfil de velocidade não se altera ao longo do tubo. A pressão diminui (linearmente) ao longo do tubo para “empurrar” o fluido através do tubo e superar o atrito. Usando o método das variáveis repetidas, desenvolva uma relação adimensional entre a queda da pressão Δ P = P 1 - P 2 e os outros parâmetros do problema. Verifique se modificou seus grupos π adequadamente para chegar aos parâmetros adimensionais usuais e cite-os. (Sugestão: por questões de consistência, selecione D em vez de L ou e como um de seus parâmetros repetidos.)

Passo 1

O enunciado pede a relação entre a queda de pressão Δ P e os parâmetros independentes.

Então vamos começar reunindo os parâmetros dimensionais que descrevem o problema!

Δ P = f ( V , ε , ρ , μ , D , L )

Daqui a gente já consegue ver o número de parâmetros:

n = 7

Passo 2

Agora a gente precisa listar as dimensões primárias de cada parâmetro!

{ Δ P } = { m 1 L - 1 t - 2 }

V = { L 1 t - 1 }

ε = { L - 1 }

{ ρ } = m 1 L - 3

μ = { m 1 L - 1 t - 1 }

D = { L 1 }

L = { L 1 }

Passo 3

Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões m ,   L e t , então podemos considerar:

j = 3

Teorema de Pi de Buckingham:

k = n - j

O n a gente já tinha achado no Passo 1, lá vimos que n = 7 !

Substituindo:

k = 7 - 3 = 4

Nesse caso o número de grupos π esperado é igual a 4. Então vamos atrás deles!!

Passo 4

Antes de começar a precisamos decidir quais vão ser os 3   parâmetros repetidos.

Aqui nós não podemos escolher o parâmetro Δ P por ele ser uma variável dependente, dos parâmetros ε ,   D e L nós só podemos pegar um, já que eles tem exatamente a mesma dimensão, desses a gente vai escolher o D já que o enunciado deu essa dica pra a gente!

Além de D vamos escolher também V e ρ !

Passo 5

Agora sim, vamos encontrar o nosso primeiro grupo π !!

Começando com o π 1 que vai ser o π dependente!!

Organizando os nossos parâmetros a gente fica com:

π 1 = 1 = { ( Δ P ) × ρ a × V b D c }

Escrevendo suas dimensões básicas:

π 1 = m 0 L 0 t 0 = { ( m 1 L - 1 t - 2 ) × m 1 L - 3   a × L 1 t - 1 b L c }

Agora equacionando:

Massa:

m 0 = m 1 × m a

0 = 1 + a

a = - 1

Comprimento:

L 0 = L - 1 × L - 3 a × L - b × L c

0 = - 1 - 3 a + b + c

0 = - 1 + 3 + b + c

Tempo:

t 0 = t - 2 × t - b

0 = - 2 - b

b = - 2

Logo:

0 = - 1 + 3 + b + c

0 = - 1 + 3 - 2 + c

c = 0

Substituindo a , b e c , temos:

π 1 = { ( Δ P ) × ρ - 1 × V - 2 D 0 }

Organizando:

π 1 = Δ P ρ V 2

Esse é o número de Euler!  

Agora vamos achar π 2 , esse vai ser nosso primeiro π independente combinando as nossas variáveis repetidas com μ :

π 2 = 1 = { ( μ ) × ρ d × V e D f }

Escrevendo suas dimensões básicas:

π 1 = m 0 L 0 t 0 = { ( m 1 L - 1 t - 1 ) × m 1 L - 3   d × L 1 t - 1 e L f }

Agora equacionando:

Massa:

m 0 = m 1 × m d

0 = 1 + d

d = - 1

Comprimento:

L 0 = L - 1 × L - 3 d × L e × L f

0 = - 1 - 3 d + e + f

0 = - 1 + 3 + e + f

Tempo:

t 0 = t - 1 × t - e

0 = - 1 - e

e = - 1

Logo:

0 = - 1 + 3 - 1 + f

f = - 1

Substituindo:

π 2 = 1 = { ( μ ) × ρ - 1 × V - 1 D - 1 }

π 2 = μ ρ V D

Achamos o inverso do número de Reynolds, então vamos arrumar um pouquinho e temos:

π 2 = ρ V D μ = R e

Agora vamos formar o π 3 com ε !

Pra simplificar a nossa vida, vamos pensar uma coisinha! A dimensão de ε é L - 1 , semelhante a dimensão de D que é igual a L , certo?! Então todas as outras variáveis que tiverem o expoente diferente de apenas comprimento vão ser zeradas!

Então podemos pular a parte dos cálculos e concluir que:

π 3 = ε D

A mesma coisa acontece com a variável L , então temos:

π 4 = L D

Com isso achamos todos os nossos grupos π !

Passo 6

Agora vamos escrever a relação entre os grupos π .

Δ P ρ V 2 = f ρ V D μ , ε D , L D

Ou:

E u = f R e , ε D , L D

Resposta

E u = f R e , ε D , L D

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O vertedouro de uma barragem deve ser testado usando a escala de Froude com um modelo em escala 1:30. O escoamento do modelo tem uma velocidade média de 0,6 m/s e uma vazão volumétrica de 0,05 m³/s. Q
Resolva o Problema P5.49 para glicerina a 20 o C, usando o gráfico do arrasto na esfera modificado da Figura 5.11.
O protótipo de um vertedouro tem uma velocidade característica de 3 m/s e um comprimento característico de 10 m. Um modelo reduzido é construído, usando a escala de Froude. Qual será a razão de escala
O modelo de um propulsor de navio na escala 1:40 é testado em um tanque de reboque a 1.200 rpm, exibindo uma potência de saída de 1,9 W. De acordo com as leis de escala de Froude, quais devem ser a ve
O protótipo da estrutura de uma plataforma oceânica deve enfrentar correntes de 150 cm/s e ondas com períodos de 12 s e 3 m de altura. Se um modelo na escala de 1:15 é testado em um canal de ondas, qu