Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 122
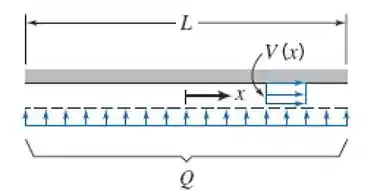
Um fluido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total por uma superfície porosa para o interior de uma pequena fresta entre placas paralelas estreitamente espaçadas, conforme mostrado. O fluido tem apenas movimento horizontal dentro da fresta. Considere escoamento uniforme através de qualquer seção vertical. Obtenha uma expressão para a variação de pressão como uma função de . Sugestão: Aplique a equação da conservação da massa e a equação da quantidade de movimento a um volume de controle diferencial de espessura , localizado na posição .
Passo 1
Tá legal! Vamos começar esse exercício ilustrando o problema e desenhando o volume de controle conforme pedido no enunciado:
Vamos começar esse exercício aplicando o princípio da continuidade para o sistema, nesse caso, teremos:
Então, nesse caso, aplicando para o volume de controle desenhado, sabendo que o escoamento se dá em regime permanente, então podemos cancelar a derivada no tempo, temos:
Então, podemos cancelar o termo que aparece duas vezes e com sinal oposto, podemos também dividir os dois lados da equação por , então, ficamos com:
Então, integrando essa expressão de maneira indefinida, temos:
Para obter o valor da constante , podemos assumir que em , então, dessa forma:
E a equação da velocidade em função de se torna:
Passo 2
Agora vamos aplicar a equação 4.18a apresentada nessa seção do equilíbrio de momento, para o volume de controle do passo 1:
Como o escoamento se dá em regime permanente, então a derivada no tempo será zero, e como não temos força de campo atuando na direção , então , dessa forma, a equação se torna:
E, nesse caso, temos , e , então, substituindo os valores conhecidos:
No entanto, como vimos no passo 1 através da continuidade, temos:
Então, substituindo essa exressão na equação anterior, temos:
O termo aparece duas vezes do lado direito com o sinal trocado, da mesma forma que o termo do lado esquerdo, então, simplificando a expressão, temos:
Sabemos que a multiplicação entre dois infinitesiais, nesse caso, e dá um número muito pequeno, que podemos desprezar, então, a equação acima se torna:
Passo 3
Agora, vamos isolar da equação obtida no passo 2, então, temos:
E, conforme vimos através da equação de continuidade do passo 1, temos que:
E que a velocidade será:
Então, substituindo essas expressões na equação anterior, temos:
Agora, integrando essa equação de maneira indefinida, temos:
Para encontrar a constante , vamos adotar que, em , dessa forma, temos:
Dessa forma, a a variação de pressão em função de será dada por: