Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 200

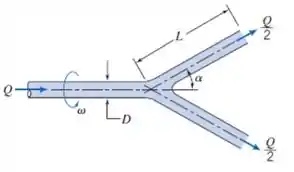
Um tubo simetricamente em duas pernas de comprimento L, e o sistema todo gira com velocidade angular ω em torno do seu eixo de simetria. Cada perna é inclinada de um ângulo α em relação ao eixo de rotação. Líquido entra no tubo em regime permanente, com quantidade de movimento angular igual a zero e com uma vazão volumétrica Q . O diâmetro do tubo, D , é muito menor que L . Obtenha uma expressão para o torque externo necessário para girar o conjunto. Que torque adicional seria necessário para imprimir uma aceleração angular ω ?

Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω ˙ × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 ;
  5. r × V = 0 .

Passo 2

Realizando as considerações:

T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω ˙ × r ρ d ∀ = 0

T e i x o = ∫ V C r × 2 ω × V + ω × ω × r + ω ˙ × r ρ d ∀

Para o tubo superior, temos que:

r = r ( cos ⁡ α k ^ + s e n   α   î ) ;

ω = ω k ^ ;

V = Q 2 A ( cos ⁡ α k ^ + s e n   α   î ) .

Substituindo na equação:

T s u p e r i o r = ∫ V C r ( cos ⁡ α k ^ + s e n   α   î ) × 2 ω k ^ × Q 2 A ( cos ⁡ α k ^ + s e n   α   î ) + ω k ^ × ω k ^ × r ( cos ⁡ α k ^ + s e n   α   î ) + ω ˙ k ^ × r ( cos ⁡ α k ^ + s e n   α   î ) ρ d ∀

T s u p e r i o r = ∫ V C r cos ⁡ α k ^ + s e n   α   î × ω Q A   s e n   α j ^ + ω k ^ × ω r   s e n   α   j ^ + ω ˙ r   s e n   α   j ^ ρ d ∀

T s u p e r i o r = ∫ 0 L r cos ⁡ α k ^ + s e n   α   î × ω Q A   + ω ˙ r   s e n   α j ^ - ( ω 2 r   s e n   α   î )   ρ A d r

Passo 3

Simplificando ainda mais a equação para obter o torque do tubo superior:

T s u p e r i o r = ∫ 0 L r cos ⁡ α k ^ + s e n   α   î × ω Q A   + ω ˙ r   s e n   α j ^ - ( ω 2 r   s e n   α   î )   ρ A d r

T s u p e r i o r = ∫ 0 L ω Q r A + ω ˙ r 2 cos ⁡ α s e n   α   - î + ω Q r A + ω ˙ r 2 s e n 2   α   k ^ + ω 2 r 2 cos ⁡ α s e n   α   ( - j ^ ) ρ A d r

Integrando:

T s u p e r i o r = ω Q L 2 2 A + ω ˙ l 3 3 cos ⁡ α s e n   α   - î + ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α   k ^ + ω 2 L 3 3 cos ⁡ α s e n   α   ( - j ^ ) ρ A

Passo 4

Para o tubo inferior:

r = r ( cos ⁡ α k ^ - s e n   α   î )

Então:

T i n f e r i o r = ∫ V C r ( cos ⁡ α k ^ - s e n   α   î ) × 2 ω k ^ × Q 2 A ( cos ⁡ α k ^ - s e n   α   î ) + ω k ^ × ω k ^ × r cos ⁡ α k ^ - s e n   α   î + ω ˙ k ^ × r ( cos ⁡ α k ^ - s e n   α   î ) ρ d ∀

T i n f e r i o r = ∫ V C r cos ⁡ α k ^ - s e n   α   î × - ω Q A   s e n   α j ^ + ω k ^ × - ω r   s e n   α   j ^ - ω ˙ r   s e n   α   j ^ ρ d ∀

T i n f e r i o r = ∫ 0 L r cos ⁡ α k ^ - s e n   α   î × - ω Q A   + ω ˙ r   s e n   α j ^ + ( ω 2 r   s e n   α   î )   ρ A d r

Passo 5

Simplificando ainda mais a equação para obter o torque do tubo inferior:

T i n f e r i o r = ∫ 0 L r cos ⁡ α k ^ - s e n   α   î × - ω Q A   + ω ˙ r   s e n   α j ^ + ( ω 2 r   s e n   α   î )   ρ A d r

T i n f e r i o r = ∫ 0 L ω Q r A + ω ˙ r 2 cos ⁡ α s e n   α   î + ω Q r A + ω ˙ r 2 s e n 2   α   k ^ + ω 2 r 2 cos ⁡ α s e n   α   j ^ ρ A d r

Integrando:

T i n f e r i o r = ω Q L 2 2 A + ω ˙ l 3 3 cos ⁡ α s e n   α   î + ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α   k ^ + ω 2 L 3 3 cos ⁡ α s e n   α   j ^ ρ A

Passo 6

Para calcular o torque total, temos:

T e i x o = T s u p e r i o r + T i n f e r i o r

T e i x o = ω Q L 2 2 A + ω ˙ l 3 3 cos ⁡ α s e n   α   - î + ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α   k ^ + ω 2 L 3 3 cos ⁡ α s e n   α   ( - j ^ ) ρ A + ω Q L 2 2 A + ω ˙ l 3 3 cos ⁡ α s e n   α   î + ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α   k ^ + ω 2 L 3 3 cos ⁡ α s e n   α   j ^ ρ A

T e i x o = 2 ρ A ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α k ^

Passo 7

Obtendo uma expressão para o torque externo necessário para girar o conjunto:

Em estado estacionário:

T e i x o = 2 ρ A ω Q L 2 2 A s e n 2   α k ^

T e i x o = ρ ω Q L 2   s e n 2   α k ^

Que torque adicional seria necessário para imprimir uma aceleração angular ω :

T e i x o = 2 ρ A ω Q L 2 2 A + ω ˙ l 3 3 s e n 2   α k ^

T e i x o = 2 ρ A ω ˙ l 3 3 s e n 2   α k ^

T e i x o = 2 ρ A ω ˙ l 3 3 s e n 2   α k ^

Resposta

T e i x o = ρ ω Q L 2   s e n 2   α k ^

T e i x o = 2 ρ A ω ˙ l 3 3 s e n 2   α k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma turbomáquina simples é constituída de um disco com dois dutos internos que saem tangencialmente através de seções quadradas, como na Figura P3.117. Água a 20°C entra perpendicularmente ao disco no
No Problema P3.60, encontre o torque em torno do flange 1 se o ponto central de saída 2 está a 1,2m diretamente abaixo do centro do flange.
Um jato de água de 3 cm de diâmetro atinge uma placa normal, como na Figura FE3.5. Se a força necessária para escorar a placa é de 23 N, qual é a velocidade do jato? (a) 2,85 m/s, (b) 5,7 m/s, (c) 8,1
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se a velocidade é V 2 = 8m / s e o atrito é desprezado, qual é a força axial no flange, necessária para manter o bocal fixado ao
Um jato de álcool atinge a placa vertical da Figura P 3.149 . Uma força F ≈ 425N é necessária para manter a placa estacionária. Considerando que não há perdas no bocal, calcule (a) o fluxo de massa de