Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 89
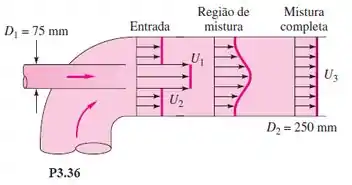
Considere a Figura P3.36 como um problema geral de análise de uma bomba ejetora de mistura. Se todas as condições são conhecidas nas seções 1 e 2 e se o atrito na parede é desprezível, deduza fórmulas para calcular (a) e (b) .
Passo 1
Bora pra mais uma!
Vamo utilizar uma conservação de massa, assim:
Desenvolvendo,
Isolando , temos a resposta da alternativa (a), assim:
Passo 2
Para (b), vamos aplicar uma relação de momento em x, assim, vamos assumir que , logo:
Vamos substituir a equação encontrada em (a) na nossa relação de momento e isolar , assim:
Resposta
Exercícios de Livros Relacionados
Água escoa em regime permanente pelo bocal de uma mangueira de incêndio. A mangueira tem diâmetro interno de 75m m e a ponta do bocal de 25m m ; a pressão manométrica na mangueira é 510k P a e a corre
Um tipo de prato, raso e circular, tem um orifício de bordas vivas no centro. Um jato de água, de velocidade V , atinge o prato concentricamente. Obtenha uma expressão para a força externa necessária
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.38, se a profundidade normal ao diagrama for w = 1m .
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.39. Você esperaria que a pressão na saída fosse maior, menor ou a mesma que a pressão na entrada? Por quê?
Em um experimento laboratorial, a vazão de água deve ser medida capturando-a conforme a água sai verticalmente de um tubo dentro de um tanque aberto e vazio que está sobre uma balança zerada. O fundo