Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 1.Problemas - Ex. 13
Qual é a forca líquida que atua sobre um automóvel trafegando com velocidade constante de (a) numa estrada plana e (b) numa estrada morro acima?
Passo 1
Primeiro o exercício quer saber a força líquida aplicada sobre um automóvel que está andando a uma velocidade constante numa estrada sem inclinação. Essa força líquida que o enunciado quer saber é apenas a força resultante aplicada ao carro. Em outras palavras, ela é a soma de todas as forças externas aplicadas nele.
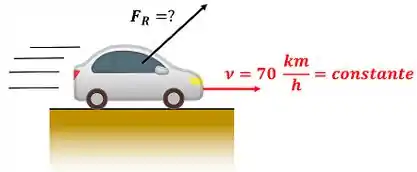
A figura acima mostra os dados que temos para descobrir o valor da força resultante . O primeiro passo para resolver esse problema é justamente entender os dados que o enunciado nos deu: o valor da velocidade e o fato de essa velocidade ser constante.
Na próxima etapa vamos descobrir como usar esses dados para chegar no valor de .
Passo 2
Para descobrir quanto vale , precisamos lembrar da equação da segunda lei de Newton. Essa fórmula diz que a força resultante é igual à massa do carro vezes a aceleração do carro .
Como o enunciado diz que a velocidade é constante, o carro não possui aceleração. Logo, a força resultante é nula!
Passo 3
O segundo caso é bem parecido com o primeiro. O enunciado pede a força resultante de um carro que está andando a uma velocidade constante. A única diferença é que agora o carro está andando em uma estrada inclinada. A figura abaixo mostra os dados que temos para resolver essa questão.
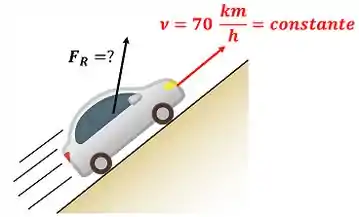
Passo 4
Novamente, para descobrir quanto vale , precisamos lembrar da equação da segunda lei de Newton. Essa fórmula diz que a força resultante é igual à massa do carro vezes a aceleração do carro .
Como o enunciado diz que a velocidade é constante, o carro não possui aceleração. Logo, a força resultante é nula!