Um forno é construído em três seções, que incluem uma seção circular isolada termicamente (2) e uma seção cilíndrica também com isolamento (3), assim como uma seção cilíndrica intermediária (1) que tem aquecedores elétricos nela embutidos. O comprimento total e o diâmetro são de e , respectivamente, e as seções cilíndricas têm comprimentos iguais. A vizinhança encontra-se a .

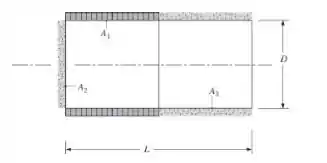
(a) Se todas as superfícies forem negras, determine a potência elétrica, , necessária para manter a seção aquecida a

(b) Quais são as temperaturas das seções isoladas e ?

(c) Para gere um gráfico de e como funções da razão comprimento-diâmetro, no intervalo .

Para resolver essa questão vamos assumir:

(1) Todas as superfícies são pretas;

(2) As áreas (1, 2, 3) são isotérmicas;

(3) Radiosidade e irradiação uniformes da superfície.

Para completar o gabinete representando o forno, vamos definir a superfície hipotética como a abertura em (lado direito) com emissividade de unidade.

Para cada uma das superfícies 1, 2 e 3 do gabinete, o equilíbrio de energia segue:

Onde os poderes emissivos são,

Para este gabinete de quatro superfícies, há fatores de forma e.

Deve ser determinado diretamente (por inspeção ou fórmulas) e o restante pode ser avaliado a partir da regra de soma e relação de reciprocidade. Por inspeção,

Na relação de disco paralelo coaxial, Tabela 13.2, encontramos

Então,

Considerando o gabinete de três superfícies e encontrando como começando com a regra de soma,

Onde, por simetria, e usando reciprocidade,

E da regra de soma em

Usando a relação de disco paralelo coaxial, Tabela 13.2, para encontrar ,

Então,

Avaliando encontramos,

E avaliando encontramos,

Por simetria, temos que:

e

Até este ponto, determinamos diretamente seis fatores de forma e o restante pode ser avaliado a partir das regras de soma e das relações de reciprocidade apropriadas.

Conhecendo todos os fatores de forma necessários, os balanços de energia e as potências emissivas, podem ser resolvidos simultaneamente para obter: